These pages are meant to help you make a map. Yourself. No Google. No electronics.
Just a Pizza Box. Some straight pins. A pencil. A ruler. And something to make a map of.
-
(Those are the essentials. (Something like a pizza box will do for that.) Of course, some other "bits and pieces" would be useful. They will be mentioned as they arise in this story.)
A medium sized field will do. And it maybe the place to start. But if you can find two hills, or two places on a convex waterfront, where you can get to both hilltops, both "places" and see each from the other, anything you can see from both can go on your map.
I've done this exercise with hilltops which are 2 miles apart. I have things on my map that are 15 miles and more from the hilltops. And they are probably in the right place to within about 50 feet. Okay, I "went fancy" and added "a thing"... but it cost less than $25. (And $15 of that was an eBay air rifle telescopic sight.)
Pizza box and pins? I'd guess I could still achieve a 200 square miles map with things in the right places to within 500 feet. I'll have to try it! (I've done similar things, but can't, off the top of my head, tell you exactly how big the mapped area or the error was.)
This is something You Can Do.
And when you've done it, you can check how close your map comes to what is in the real world.
If you aren't satisfied with your first attempt, you get an extra Thing You Can Do... Can you figure out what you need to do differently to get a map that agrees with the real world better?
Or you can stick your nose in your smartphone and be a sack of potatoes.
"What good is it"? I don't know. If I gave you a screwdriver, I don't know what good that would be. But if you have it, it might be useful. If you try this challenge it might be fun, and also you might strengthen some important general skills along the way. Have you got something better to do today?
(If this version isn't quite to your taste, please give my old version a try? It is more polished... but less complete! You can go there directly with https://bit.ly/MakeMyMap,
or with http://www.arunet.co.uk/tkboyd/MappingArms.htm
-
(The page you are reading is easily accessed with https://bit.ly/MakeMyMap3, remember, if you are feeling kind and would pass that on to people?))
Okay... you aren't going to put maps.google.com or the sat nav makers out of business. But you will have the beginnings of a map, made the way they were made by even the top people, until about the 1960s. Made without any electronics. No Google. No GPS.
The way maps were made from about 1600. (Click here for Wikipedia article)
Runners run the same race, over and over, trying to get a better time. Soccer players shoot goal kick after goal kick, trying to get better. Wordle players try again and again, to get better at finding the secret word. (By the way- try Quordle... even better!)
YOU could try this map thing a few times. See if you can make a better map when you've had a little experience. (If you read all that follows carefully, you'll discover that my first attempts at the particular problem used as an example here were a little disappointing... but they were, to me, interesting: WHY didn't my results agree with each other? With what maps.google.com said I "should" get? How could I get results that agreed more closely, next time? Which bits did I do "too carefully"? Which bits was I fussing about overmuch?
(You MAY use maps.google.com to see if your map is accurate! (Notice I didn't say "... see if it is good". It can be good, even if it isn't accurate. Always remember that no one is "good" at arithmetic or spelling or any such things. You maybe fast, or accurate, or whatever. But if you are not fast or accurate, it doesn't say much about whether you are "good".
ANYWAY....
(By the way... if it isn't convenient to go outside just now, have a look at my Quickstart / Help for Chichester people page... it will "save" you having to go outside. (And it will save Chichester people from having to visit a second hill.) But try to do the exercise with your own data someday!!)
We'll do one in a medium sized open space, for practice. Even a large room will do. But two hills, or places on a river, lake or sea shore are more fun!
In a room, you might want to use two small tables. In a field, if you can put two stakes in the ground, that's idea, but all that you need, is some way to mark two spots.
These two spots are the ends of your BASELINE. I'll call them "A" and "B" from now on.
You need to be able to see A from B and B from A. Not hard!
Your map will start as a piece of paper... largish is good... and you can do the "on the paper" bit on the back side of the pizza box, of you want to be difficult about me saying "You only need..."
You'll put two dots on it. They show "A" and "B". You can put them ANYWHERE. But if you put them in some places, you're going to have to stick more bits of paper to you first bit of paper to finish your map. As you do this exercise, you'll get clever about where to put the first two dots, if you THINK about things as you go along.
Well, We DO, really! It shows "A" and "B"!!!
Okay. Maybe not whoopee just yet. It IS a map, but a pretty pathetic map.
Add to the room either put another small table, or a chair or a standard lamp... ANYTHING! (or just use something already there. Some of the CORNERS of the room are worth using.)
Or add to the field another stake or use a tree or fencepost.
Call it "C".
And don't even need to go anywhere near it!
In "real" map making, "C" may be a long way away from A and B. Or across a river. Etc.
You have to be able to SEE C from A and from B. Choose a specific bit on C, if it is something large, like a chair or a tree.
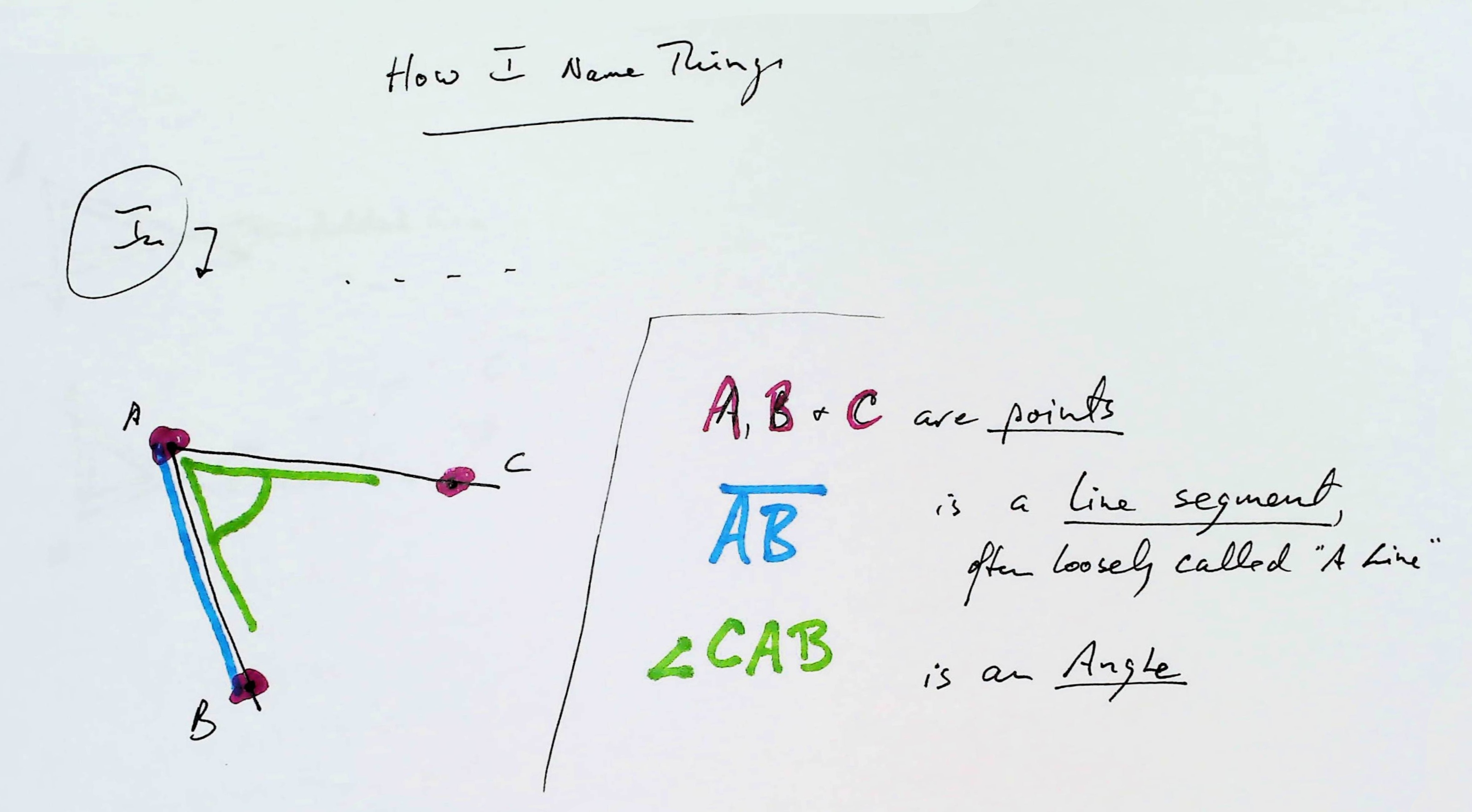
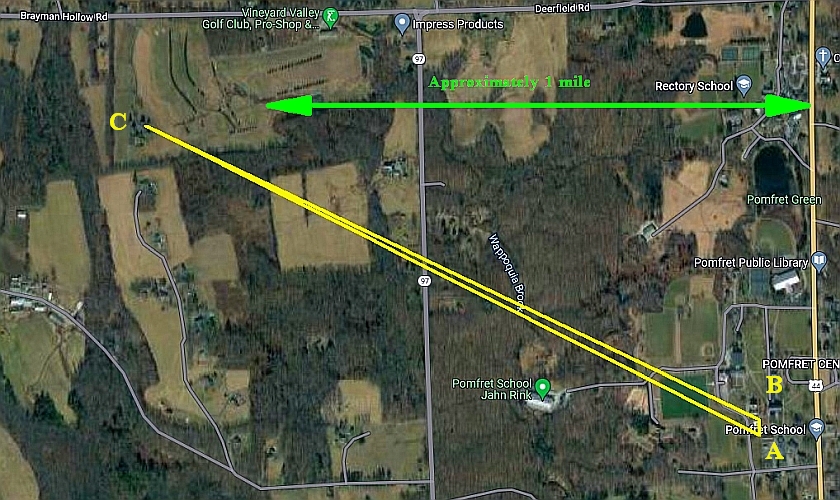
Later, we will discuss an attempt to use what is presented here to figure out how far away the left hand end of the yellow triangle is from the relatively short baseline, which you can just about see at the right hand side of the triangle shown. (There's a valley between the left and right hand sides of the image below... Pomfret School is at 41.8851, -71.9627, aka https://what3words.com/roadways.besides.atoms). (In this page, references to the "very acute yellow angle" refer to this mapping/ measuring challenge.)

I've now done the the exercise suggested above twice. The newest explaination of how that yellow triangle can be plotted, measured was done in May 2023.

In your mind's eye, imagine yourself standing at B. With one arm pointing to A and the other pointing to C. Your arms make an ANGLE, don't they?...
In a moment I will show you how to "capture"/ measure that angle.
Please note: These images, taken from over the kid's heads, are just for a preliminary discussion of the method. They were not at the place where the very acute yellow angle was captured.

You then go to A, and point one arm back to where you were a moment ago (B) and again point your other arm at C. And you get another angle. "Capture"/measure that. (It's what the pizza box and the pins are for.)
Now draw those angles on your map!
The "points" of the angles will be at A and B. The line that makes one side of the first will go from B to A. The line that makes one side of the second will go from A to B.
WHERE THE LINES OF THE OTHER SIDES OF THE ANGLES CROSS IS WHERE "C" IS on your MAP!! (^_^) (^_^)
They let you "capture" the two angles.
Turning to whatever challenge you have set yourself...
Go to one of the places you have chosen for A or B. For the purposes of this essay, we'll assume that you went to B first.
(It doesn't matter which one you do first. You knew that? Or could have done the thinking to see it without being told?)
Prop it on something very steady. It wants to be close to horizontal.
This is one of the places where having... or learning- through- this- exercise!... craft(man)ship will pay off. The CraftHumans among you will get maps that more closely match the real world than those of you with less craftpersonshipness.
Remember: You are doing this at "B".
Put a pin in to pizza box, near a corner would be best, for the place you are. The pin is to be one end of a "gunsight". In a perfect world, the pin would be exactly over the spot that is "B". Does it being a little off matter? In all of this, some things are critical to getting a result that matches the real world, other things don't need as much care. Getting the angles right is critical.
Sight across the top of the pizza box towards "C".
Put a second pin in, as far from the first as you can get it. Put it on the line that goes from your eye, to the first pin, and also to "C". (With these two pinholes, you have marked the line from "A" towards "C" on the pizza box top, haven't you?)
Assuming you are at B, put a third pin in, as far from the first as you can get it. This one must be on line from your eye, to the first pin, and thence towards "A".
The holes from those three pins define, they "capture" the angle, don't they? (Still thinking, I hope?)
The angle that you have just captured from B would be called "angle ABC", wouldn't it? (If that isn't clear to you, go back to what I said near the start of this.
Now we will move on. Next we will capture angle BAC, from A.
Here is a quick diagram to "re-explain" bits from above, in case you are in any doubt...
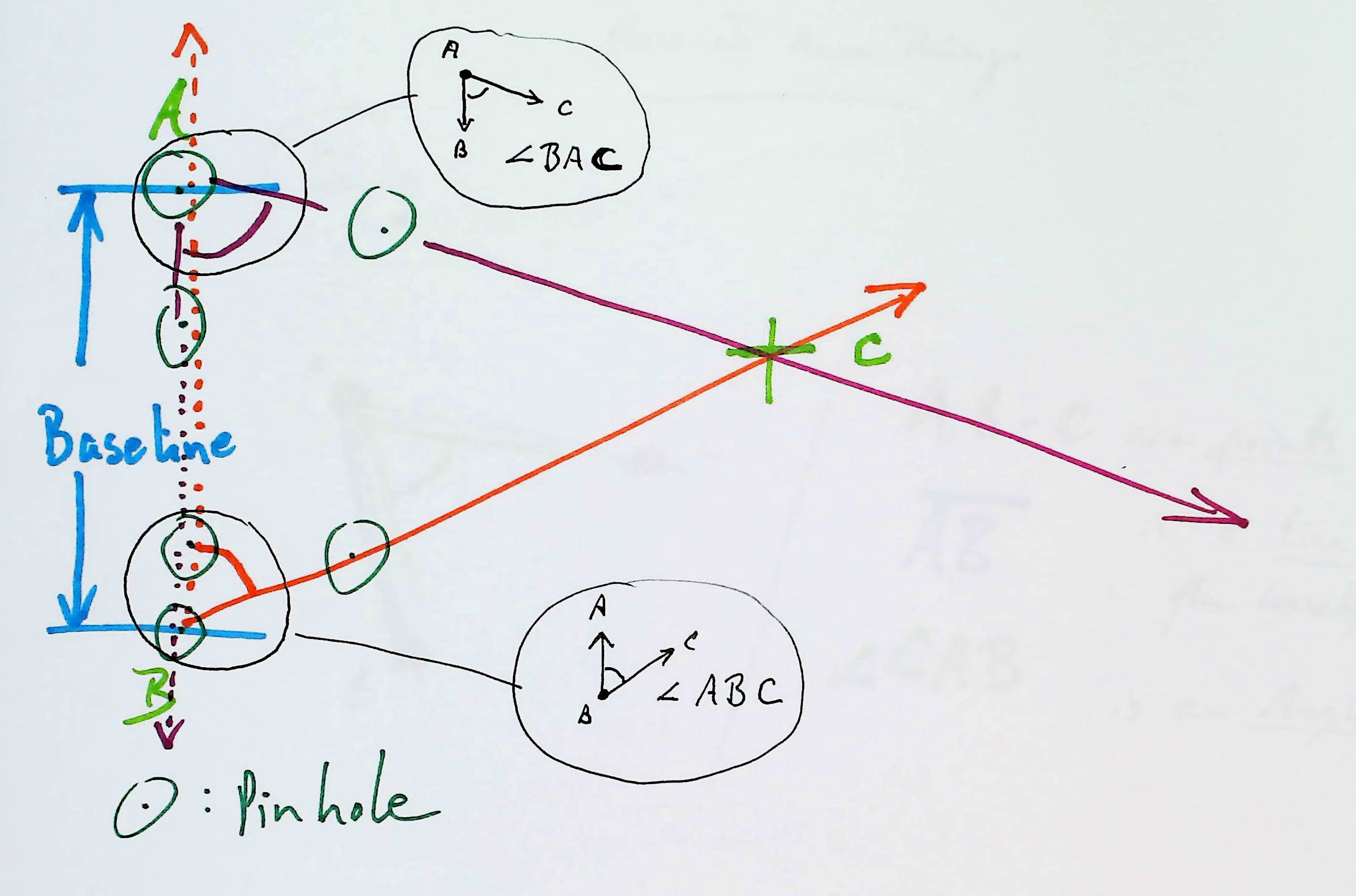
The diagram above isn't entirely ideal for when you start to think about the "acute yellow triangle" challenge. The diagram is right for that... if you realize that the diagram's north is down. Also, angle CBA in the yellow triangle challenge is obtuse (about 120 degrees), not acute, as shown in the diagram.
Don't worry! Everything still "works" as before.
============Earlier, I promised that if you tried your hand at doing this, you could then check whether you'd measured the angles accurately and drawn them accurately.
If you've only done the above, you need to use someone else's map to check your answer. Mark your A, B and C on a bit of clear plastic. Call up Google maps on a screen that is big enough to show all three of the places involved. Zoom that in and out until it is the same scale as your map... whatever that is. (We don't need to "have a number for" the scale, but we do need to match it. If your three marks line up with the places involved, your map is accurate, right? Simple! And the answer to "Did you measure and draw accurately?" doesn't depend on some teacher or parent's opinion. you can check your answer for yourself. (If you be live that the Google maps are accurate!)
Deep breath? But you don't "need" this bit, if you want to skip over it.
Can find a place you can see from A and B and C? Call it D. Repeat what you've done above, but using angles to add D to you map, with bearings to it from each of A, B and C. (For each, the "bearing" will be a measure of things like BCD- an angle you could measure from C if you could see B and D from there.
When you've measured those three angles, and drawn the three lines they dictate, the three lines towards D should all cross in the same place, shouldn't they?
(If you can't explain why they should cross in the same place, go back, think about it. You can do this!!)
Now your work checks itself!!!
You don't need anyone else's map to check whether your work has been accurate.
Unless you care about the scale (and if you do, you can have it, but it isn't part of this) or you care to have North "up" on your map (ditto), when you started drawing your map, ANY TWO DOTS would "do" for A and B. They can't be "wrong".
Then you added C. If you measured ABC and BAC correctly, and drew them correctly, C is on the right place on your map... but you can't really TELL if it is in the right place.
But when you add D, by the method explained above, if you measure the three angles for putting D on the map correctly, and draw them correctly, then the three lines for "D goes here" will ALL CROSS in the SAME PLACE!!
If they don't, there are lots of places where your could have made a mistake. With just what's given, you can't be sure where your error(s) is(were).
But! Your lines will probably nearly all cross in the same place... which would tell you that all of your measuring, all of your drawing was nearly right!
I can't tell you what a thrill it is to get three lines that cross in the same place. You have to do the work for yourself to get that reward.
Just to get away from musty theory for a moment... here's the "acute yellow angle" problem...
Below here is a "real world" picture from "A" looking towards "C", with "B" to the right of the point of view. Below that is a view from A, looking back towards B, with C a long way to the photographer's right.
Most of this page is about solving this "real world" problem. The Google Map near the top of the page, the one with the very acute yellow triangle overlaid on the "satellite" image, shows the problem. (The image shows lots of trees and fields.) We are going to measure how far C is from A and B... without ever going to C. We're going t start a map of the area. By the time we are finished, or map will show the locations of A, B and C.
N.B.: you have to "turn things around" a bit in your head. The "C"s, "B"s, and "A"s on the three images should be enough to set you straight?
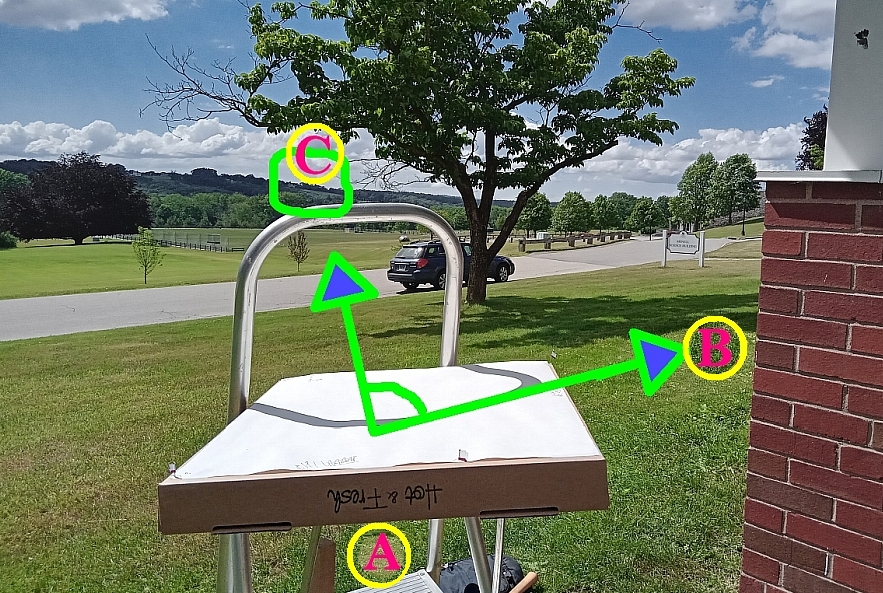
...and the following is from "B" looking towards "A"...

That's your "field work" done. You can go home now.
Take a piece of paper. This will be your final map.
Very carefully, so that you don't disturb the pinholes you made "in the field"... even if "the field" was the large indoor space!...
Transfer the first angle captured when you were at B to the map.
You map now has B on it! (If you chose well when deciding WHERE to put the point "B" on your map, the rest will be easy. If you chose it poorly, you'll have a better idea of where to put it next time, but with some extra paper and some tape or glue, you can still finish your map!)
Somewhere along the angle already on your map, on the line that stands for the line from "B" towards "A", make a dot. Or a pin hole.
Using your fieldwork, copy your angle BAC to the map, putting "B"s pinhole from the fieldwork over B's place on your map, and turning the fieldwork, until the line for "from B towards A" is on top of that line on your map.
Where....
1) the line towards C from A
...and...
2) the line towards C from B
...... CROSS is where C is on your map!! (^_^)
I've done a separate page showing my results obtained "just" by "drawing" the map more or less "directly".
I've also done a page with the gory details of using the data from the fieldwork. It shows you several ways to work out how far away "C" is.
Okay... it only show where "A" "B" and "C" are... but you would just repeat that again and again, to make your map show the location of other points of interest.
(Well, I found it amazing anyway...)
If, let's say, in the real world, A and B were 200 feet apart, and if on your map you made them 20cm apart....
THEN!... if on your map, C is 60cm from B, that TELLS YOU, without you ever having to visit C !!! that C is 600 feet from B...
Doesn't it? (Have you REALLY thought about how cool that last bit is?)
I hope you aren't wrinkling your nose in disgust? I hope you don't feel cheated?
This really is how they made maps in the grand scheme of things.
No, they didn't use pizza boxes. They had rather more expensive tools. But all those tools did, for what we are talking about, is measure angles. You can, for very little money, make better tools. (I am going to talk about (or have talked about) that in other pages.)
They had fancier ways of drawing the angles, while making the maps. Some of which I am going to talk about (or have talked about) in other pages.
But I have to stop here for the moment... apart from a few things...
This page was new, 13 June 22. I've written about these things for MANY years. I hope this attempt is better?
The details of my inexpensive angle measurerI've recently completed doing a map, using exactly what you see above. With a 43m baseline, I managed to (almost) do a map showing a tower 1950m away. (I say "almost", because according to my map it is only 1100m away. Yes- disappointing. But it was my first attempt at this one! And YOU TRY doing this with a 43m baseline and a 1950m- away "C". Getting as "close" as 1100m was, I think, pretty cool.
Other times, other (inexpensive) tools, I have gotten much closer to "exact" results". It does work... even if 1950m with a 43m baseline is "a little" ambitious.
For me doing it has been a lot of fun. Okay, I'm weird. But give it a try. There are other people in the world with my weird. Maybe you're one of them, and just haven't discovered it yet? Maybe you might find seeing if you can do a map this way fun. Can you really know, unless you give it a try? And even if it turns out that it isn't fun.. if you've made an effort to think, and to try to bring craftspersonship to the task, you will be a better thinker, a better craftsman, for the exercise you've given those things.
I would like to thank the manager of Pizzeria DaVinci, of Deep River, CT, for his kindness in giving me one of his large boxes... for free! Do offer to pay for an empty box, if your circumstances don't run to using a filled box. (Unless you are at one of the big corporation pizza places. The independent businesses around the world are on their last legs, and if you like the money earned in your community to say in your community, don't add any straws to the back of any of your local businesses.)
The details of my 43m/1950m map. (TO BE DONE YET)
The details of my inexpensive angle measurer.
Read: Latitude, by Nicholas Crane. (Not Longitude, note. The link takes you to a Goodreads page, for synopsis and reviews. Buy from Abebooks.com)
This skims through a bunch of stuff... in some places perhaps too rapidly. I've done a separate page called "After the Fieldwork", with more details of what you do with the pinholes in the pizza box to make your map. It also discussed ideas about that not even hinted at here.
THANK YOU, if you really read the above with care. I know it "goes on" a bit. It all is "very simple". That simplicity, that elegance, is a big part of what draws me to it!
But "simple to do"/ "simple in concept" isn't always so very easy to explain.
You can indeed produce quite remarkably accurate maps just with the simple "copy the angles" techniques discussed already.
However, when you are ready for some algebra and stuff, you can CALCLUATE where things ought to be, how big angles and sides of triangles "should" be.
I half suspected as much, and I knew a very experienced mathematics teacher. Knew him quite well, given that we were at school together for four years, and are what Dolly Par ton sings about in her wonderful song "Old Friends".
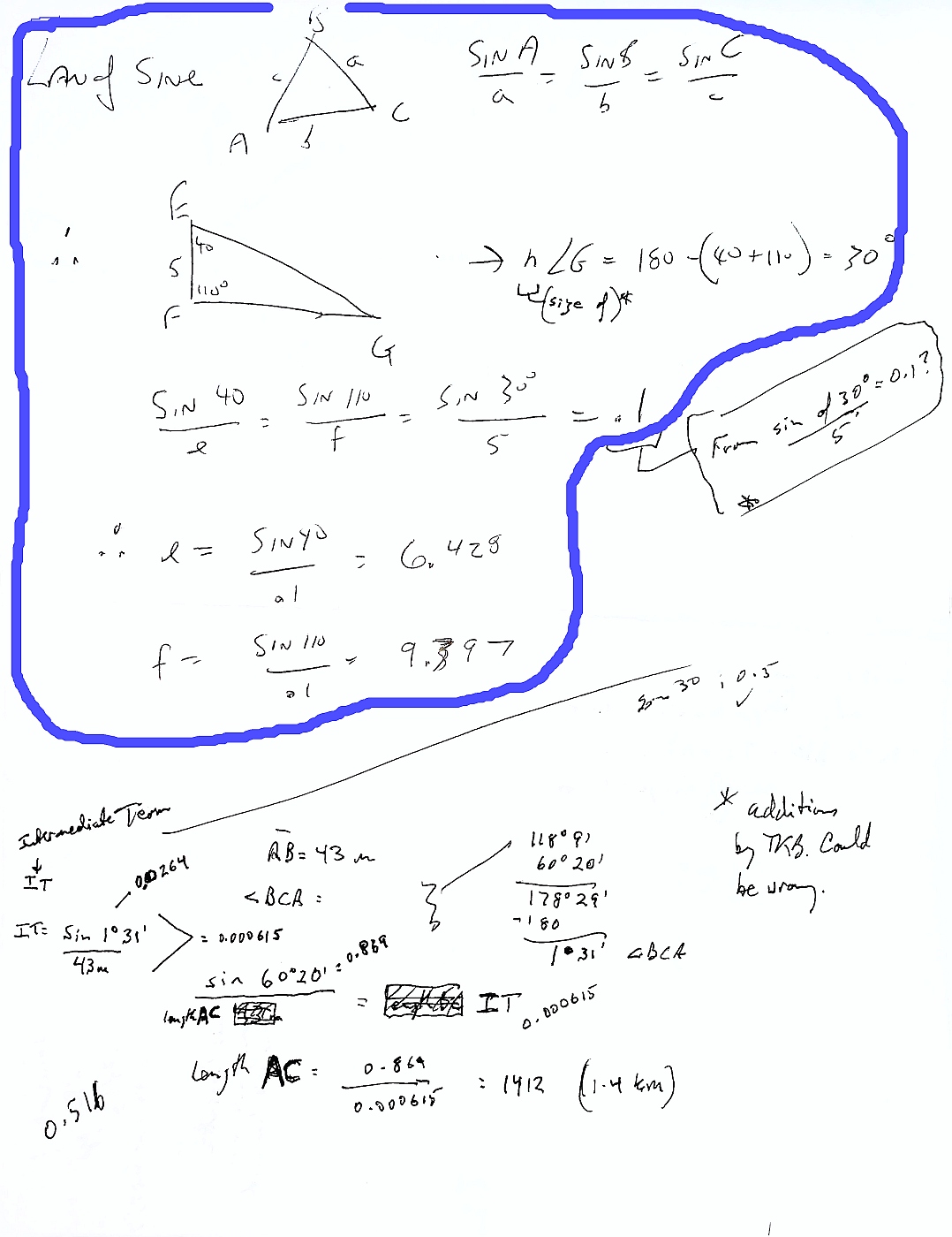
I asked him for a little help, and he said "Oh! You want the law of sines, two angles of a triangle, and the length of the side between them, and want the length(s) of one or both of the other two sides.
And then he gave me the bit circled in blue on the following, and it was my great "Eureka!" moment, and I saw how other things were possible. As explained in the page that follows on from this. (after_the_fieldwork.htm)
You may have noticed that I didn't say much about establishing the SCALE on your map. It is implied in the "If A and B were 200 feet apart in the real world, and if on your map you made them 20cm apart..."
I didn't want to distract the reader from the heart of this story with the matter of scale, not in the first pass through it.
I hope what you ought to do, to create a map with a known (and sensible) scale is clear enough.
You will need to determining the distance between your "A" and "B". For that, you can be forgiven for calling up a Google map, and using the "measure distance" tool, if your A and B are not close enough to each other to measure it directly with a ruler. Getting the scale right, for us to have fun, is not "the big deal".
Getting the scale right for "real" maps was a VERY big deal. In some ways, the longer your baseline, the better. But don't tell that to the people who have to measure it without using Google.
The book Longitude spends pages on the very real problem. You might, I hope, also enjoy, what I've written at...Roy's Hounslow Baseline.
Or at...when and how the highest point on earth was identified.
As I said... I've been having fun with all of this for a Very Long Time. Perhaps the best "index" to my stuff, at the moment, is...Flat Earth Academy- Geography Topics.
You may think I think I am a genius or something. But I don't. I'm not.
It is important to make contemporaneous notes while "doing an experiment", or making a measurement. And always to put the date (and sometimes the time, and where you were) on such things.
The idea is that you write down everything, clearly, at the time.
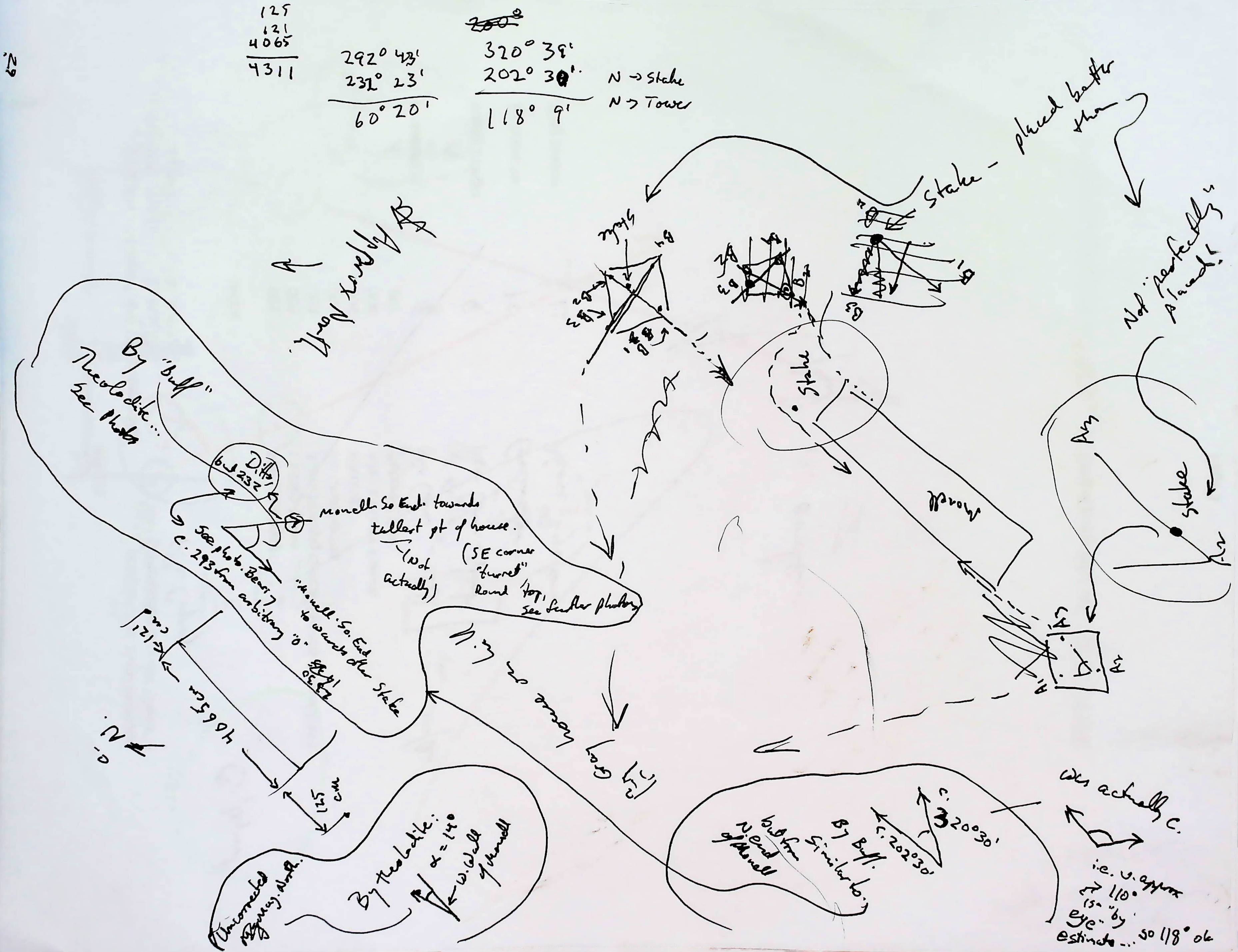
In the "experiment" we have been discussing, in my attempt to measure the distance from where I learned science as an adolescent to the hill to the west that was a fixture in my life for some important years, I failed abysmally. As you can see from the image below. I am no genius. Not of recording observations, anyway!
But- it DOES have some important data on it! Things that helped me while writing the rest of this.
I really did use a pizza box! It, specifically, is "just the thing".
I did, however, tape a large piece of paper to my pizza box. (For this, and for drawing the angle at a large scale, inexpensive "shelf paper" (or food wrapping paper or cheap wrapping paper (use the "back" side) works just fine. Don't rush off to an architectural supply store and by expensive fancy large sheets.
It's easy to measure a distance if you throw money at the problem. What can you do on a very tight budget??
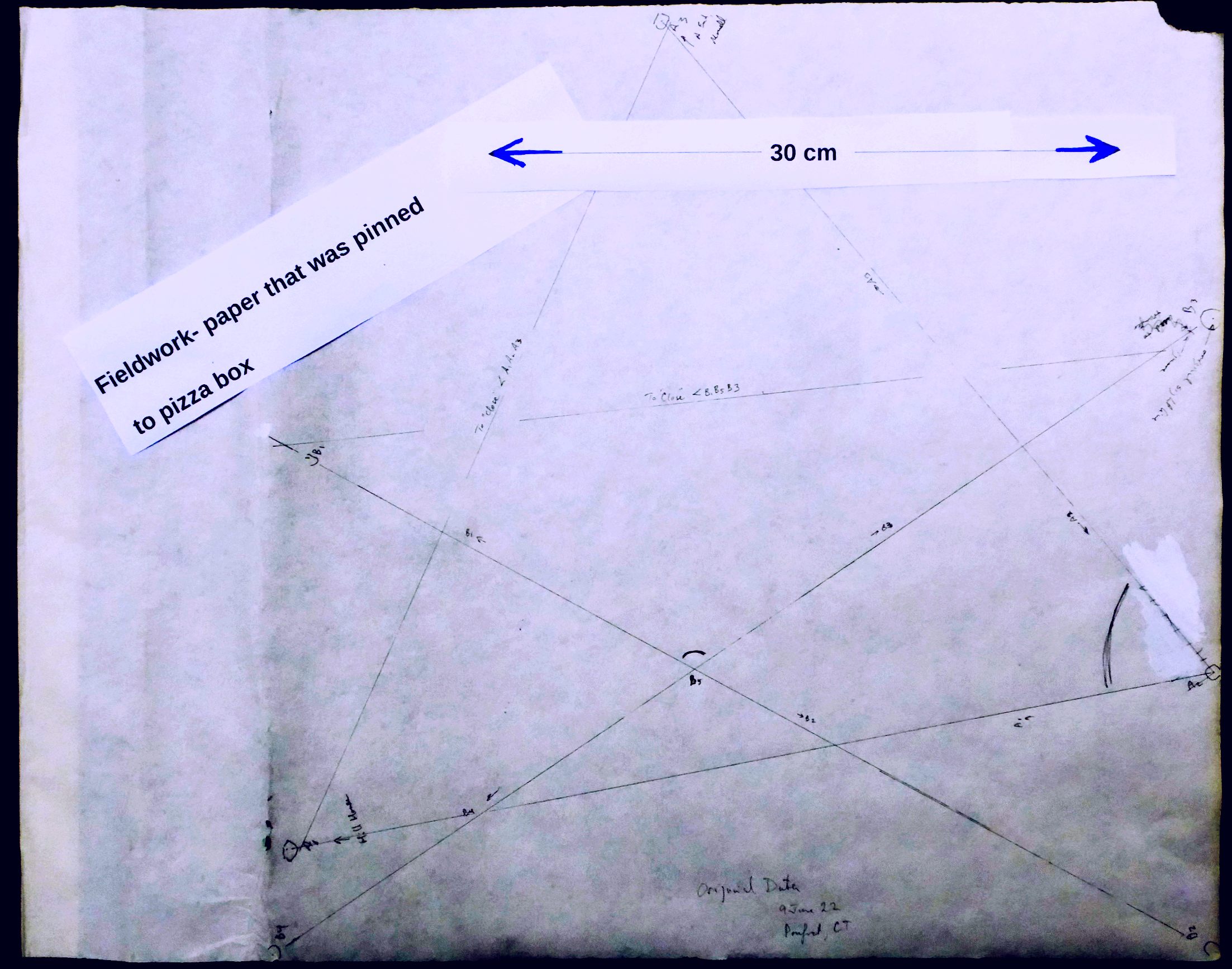
Here is my "raw data"... the marks on my "pizza box"... in three forms. The first is just what it looked like when I was through using it. The second has some highlighter to show you what I took from it along the road to determining angle CAB. The last one has marks to highlight the material relevant to angle ABC.
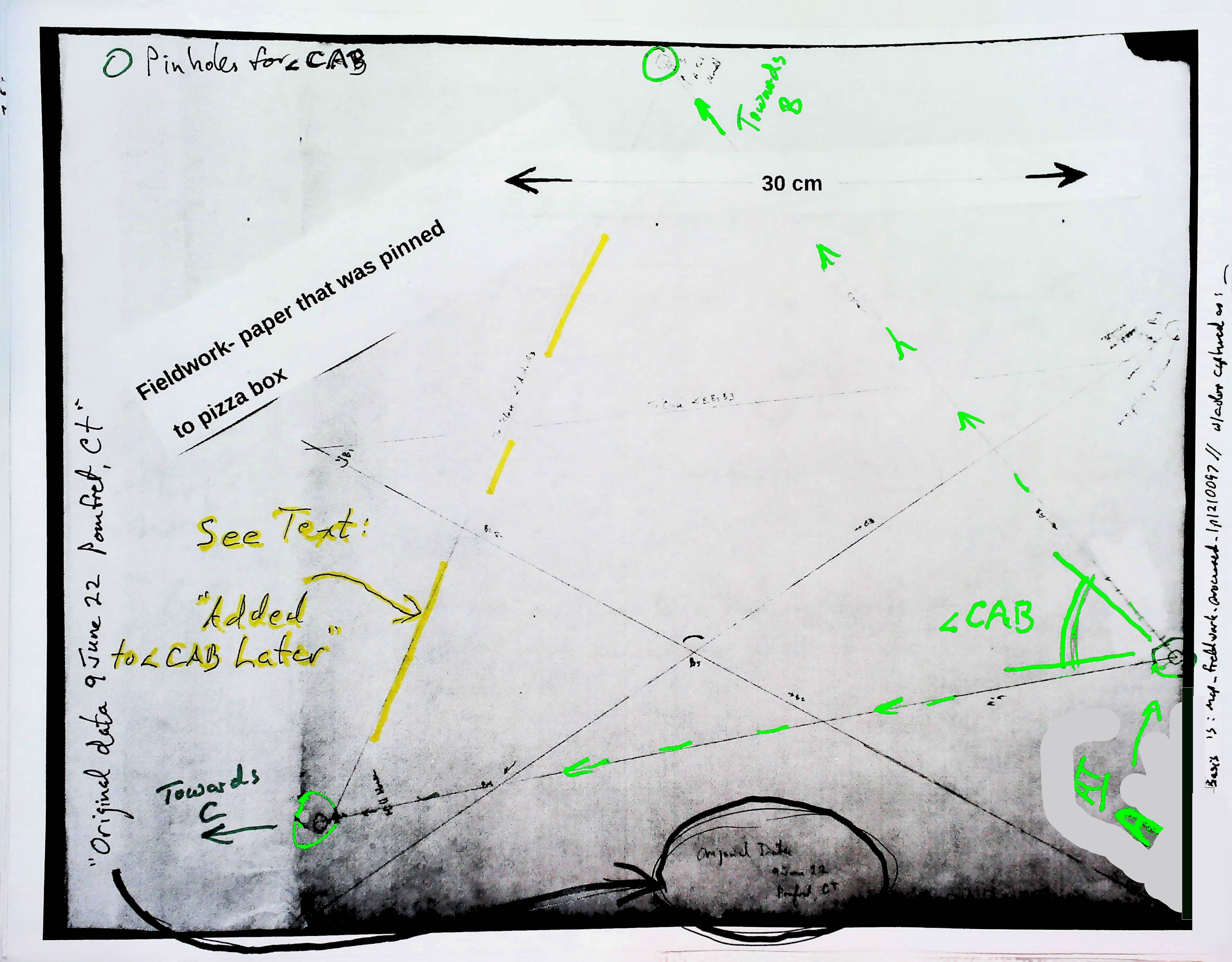
The line marked in yellow, across angle CAB, was added back at my desk, after the fieldwork was done. That line was to make the triangle which allowed the size, as a number of angle CAB to be calculated from the lengths the sides, as per the discussion above. AND that yellow line made it possible to transfer the angle to a map made by geometrical "construction" as explained above, with no need to know the angle's size as a number!
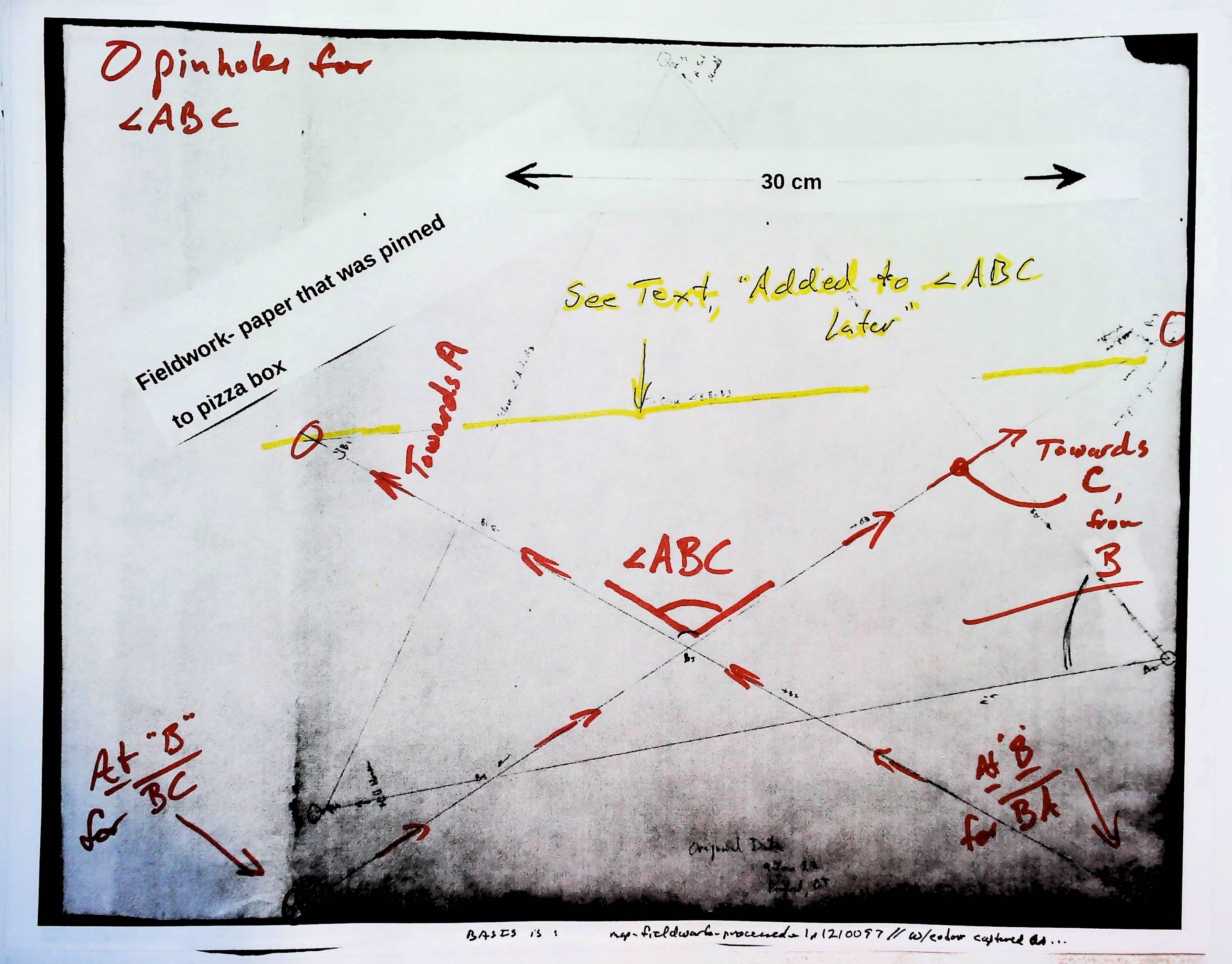
The line marked in yellow, across angle ABC, was added back at my desk, after the fieldwork was done.
It was added for the same reasons as the yellow line discussed a moment ago (the one across angle CAB in the previous image).
Why an "X" this time, not a "V"?
I didn't use just one place on the pizza box as my "I am here" place. I did two lines: one pointing to "A", the other pointing to "C"... and each from a very slightly different place. Where the lines crossed, the crossed at very, VERY nearly the angle I would have seen, had used the same pin for my "near my eye, and over the stake" pin for the "B" end of BOTH lines.
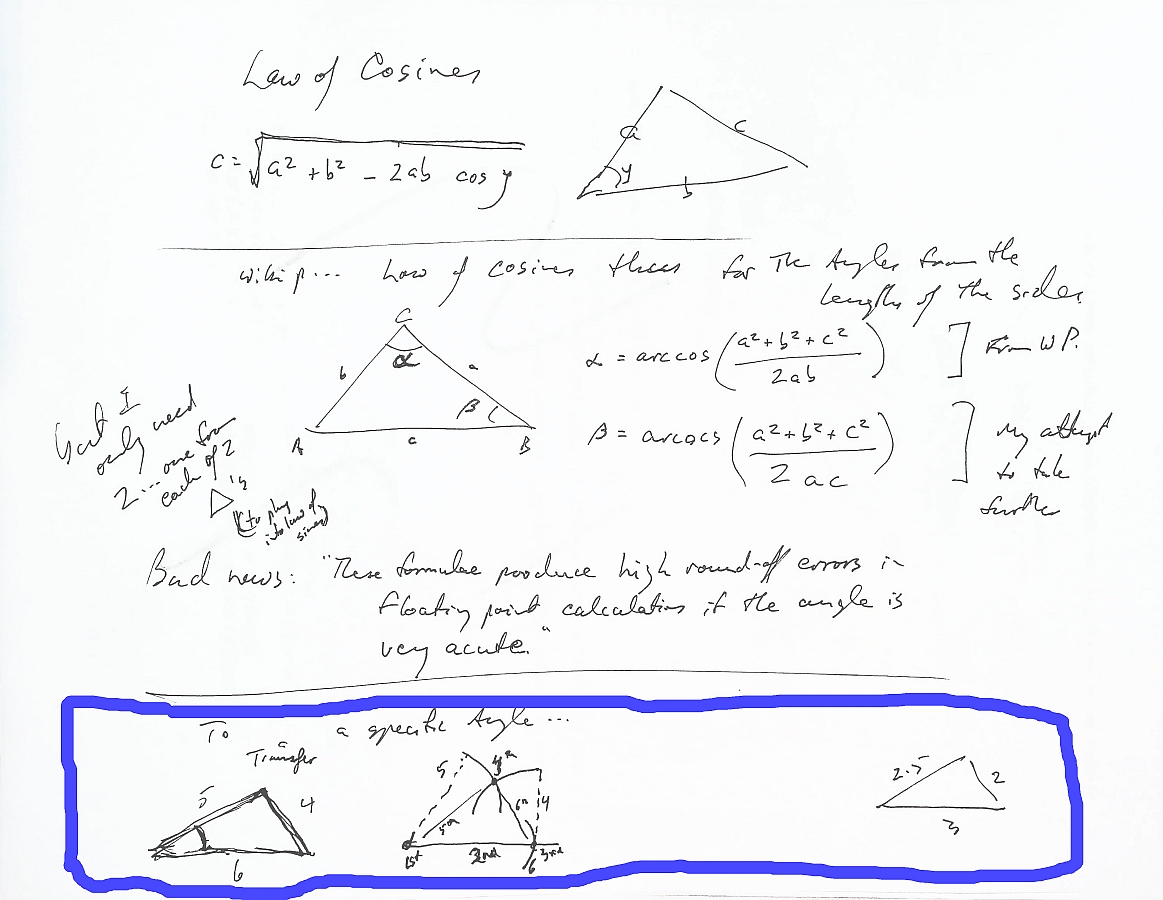
The diagram above has two things to be put somewhere more sensible. At the bottom of it, "circled" with the blue line is notes on how an angle can be "copied" with just a ruler and a compass. With a little mental arithmetic, or a calculator, if you want to do a triangle larger or smaller than the original. It is already mostly "in" these pages in a more elegant form, elsewhere.
Above that is another stab at showing you how the Law of Cosines can be used to tell you the angles in a triangle, if you know the lengths of the sides somehow. (We used this trick at least once... twice, I think, elsewhere in these pages.)
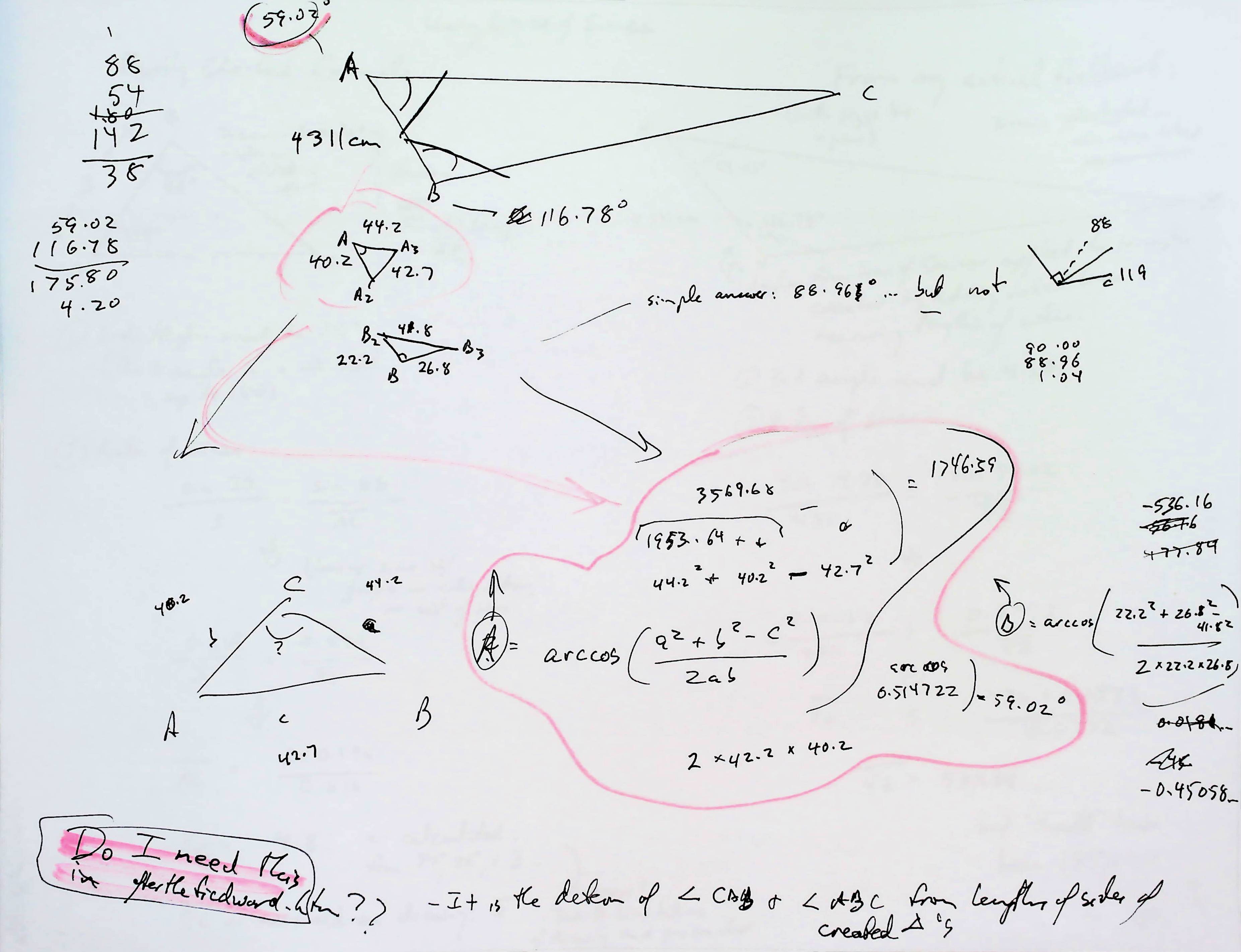
The diagram above may well be of no use! I'll have to think about it! It was one of my while figuring out the things I have presented in these pages.
On it, I first calculated the sizes of angle CBA and ABC by the "add a line to make a small triangle in corner of big triangle" trick. Then I used the law of cosines to calculate one of the lines to C from the baseline.
If you found this of interest, please mention in forums, give it a Facebook "like", or whatever. If you want more of this stuff: help!? There's not much point in me writing these things, if no one hears about them. Does anyone feel they are of any use? If YOU do- please spread the word!

... OR...
Search (only) this site...
|
Unlike the clever Google search engine, FreeFind's merely looks for the words you type, so....
* Spell them properly.
* Don't bother with "How do I get rich?" That will merely return pages with "how", "do", "I"....
Disclosure: FreeFind tells me what people have searched for. It doesn't tell me your personal details. (If someone would "spy" on you, wouldn't they also feel free to lie in a "privacy statement"? Not to say I'm not lying... how can you tell?... but to say "What are privacy statements worth?".
Please also note that I have three other sites, and that this search will not include them. They have their own search buttons.
http://www.arunet.co.uk/tkboyd/index2.htm : My site at Arunet. Only http (no httpS) accessible, I fear. It asks you for no information. Why worry on pages that ask for no information?
It's both! Flat-Earth-Academy.com is something I started years ago. For a variety of reasons, I can't offer you httpS:// access there. (As you are not asked to input any information, that's moot, but it "worries" search engines.) So I'm moving to my new, all singing, and will do the httpS:// dance site, "WYWTK.com", and Flat-Earth-Academy is gradually acquiring pages there. (Well, HERE, as what you are reading is one of my "wywtk/fea" pages.)
Why "WYWTK"? It comes from "What You Want To Know".
![]() Page has been tested for compliance with INDUSTRY (not MS-only) standards, using the free, publicly accessible validator at validator.w3.org. It passes in some important ways, but still needs work to fully meet HTML 5 expectations. (If your browser hides your history, you may have to put the page's URL into the validator by hand. Check what page the validator looked at before becoming alarmed by a "not found" or "wrong doctype".)
Page has been tested for compliance with INDUSTRY (not MS-only) standards, using the free, publicly accessible validator at validator.w3.org. It passes in some important ways, but still needs work to fully meet HTML 5 expectations. (If your browser hides your history, you may have to put the page's URL into the validator by hand. Check what page the validator looked at before becoming alarmed by a "not found" or "wrong doctype".)
. . . . . P a g e . . . E n d s . . . . .