These pages will show you how you could make a map. Yourself. No Google. No electronics.
This material started with my page "Make a Map Yourself"
-
If you tried what was presented there, you will have some data collected in the field. My other page speaks a bit about what you can do with it. This page will look at the question in more detail.
How I name things
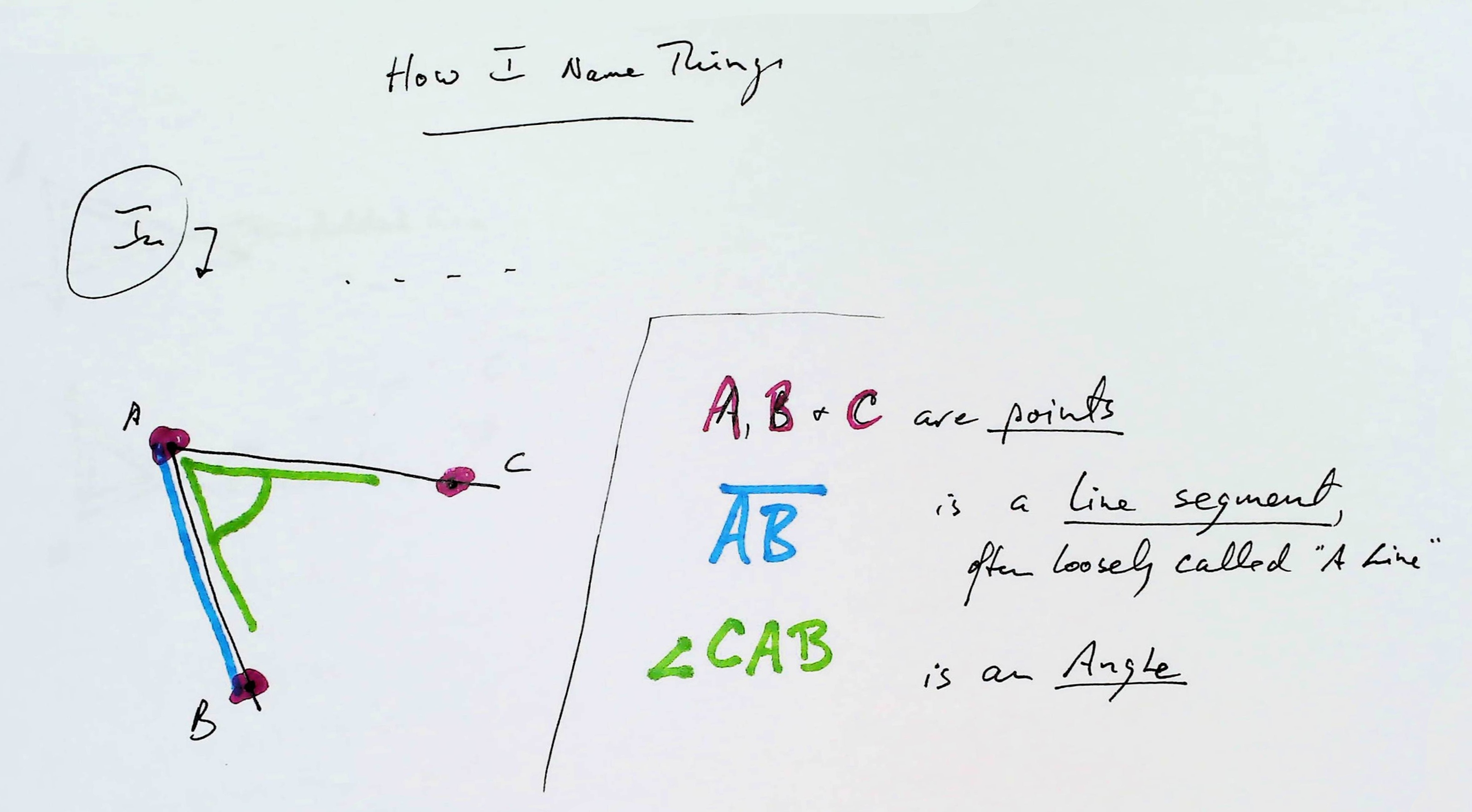
From your work in the field, you should have a number: The length of your baseline. (The line between the two places from which you captured angles.)
And you should "have" two angles, though maybe not yet... maybe never!... as numbers, but you should "have" them. (We'll come back to them in a moment.)
For the purposes of this essay, we will assume that you were only interested in "mapping" one point. Of course, such a "map" would be pretty boring, but to build a more interesting, more useful map, you just repeatedly put another point on it... by the techniques I will be discussing here.
As before: at every step in the process, be asking yourself "how critical is this bit, to getting "the right answer"? What can you do to minimize the effect of the inevitable small errors in measurements. Can you think of another way to achieve what is being done... a way less likely to introduce errors.
In the field, you had your "pizza box" (or large sheet of paper, previously stretched flat on some surface)...
And now your "pizza box" has two sets of three or four pinholes in it. Here's a not-to-scale sketch of what you come in from the fieldwork with...
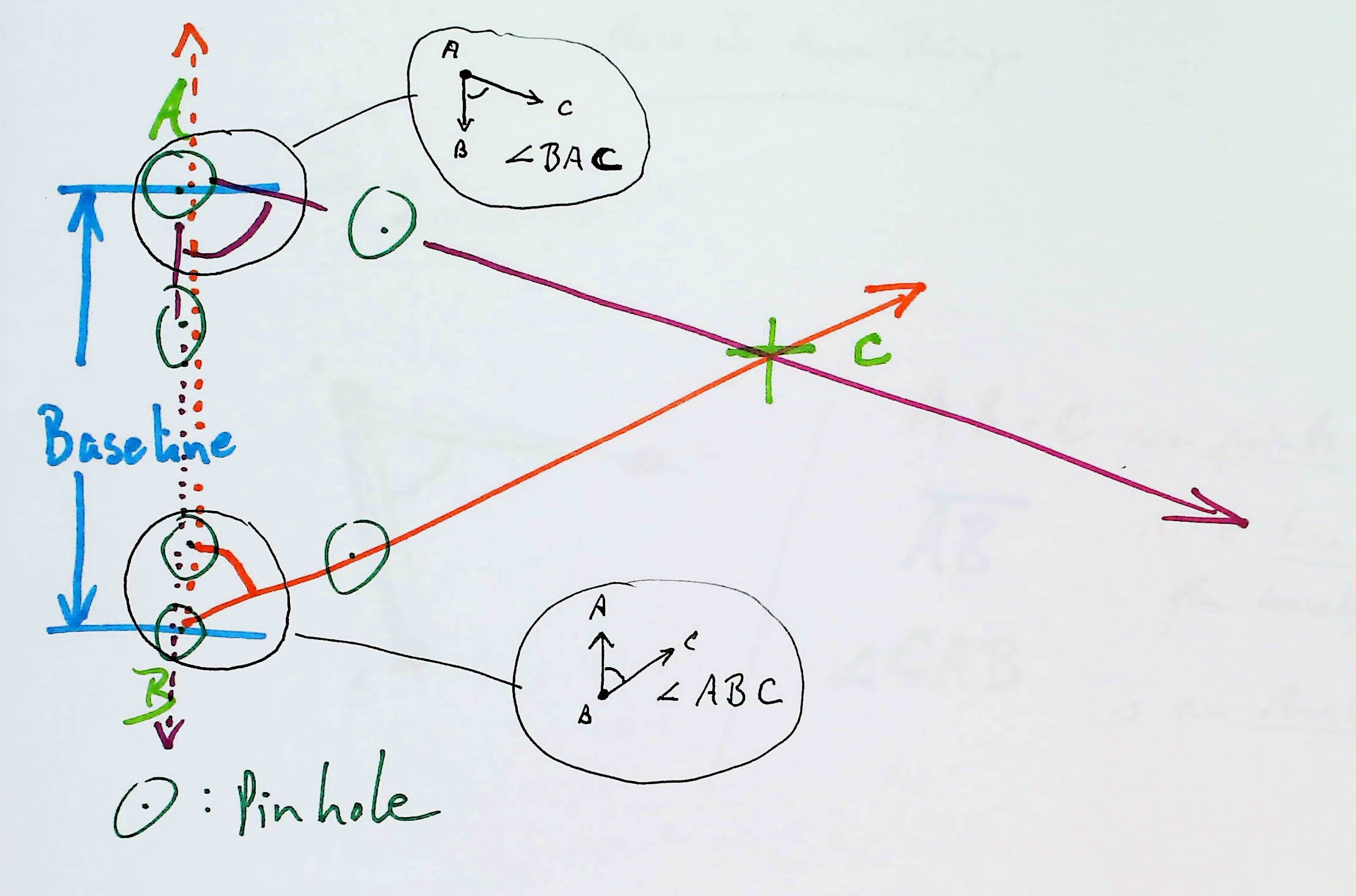
That, from left to right, is meant to show:
The pinholes are the small green dots inside the small green circles.
Those pinholes "capture" two angles, angle BAC and angle ABC. I hope "the angles" are clear, from the diagram above?
To make an accurate map from the fieldwork, you need to have put the pinholes in the right places! You need to have measured the baseline's length accurately.
You put two dots on the map you are making. They can be "anywhere", but with experience you will choose where to put them well.
If you want you map to have an easy to use scale, you do something like this...
Let's say your baseline was, as mine was in the exercise that led to this webpage, 4311cm long. (You might want to criticize that for having significance implied to too many digits.)
In that case, if you put A and B 43 cm apart on the piece of paper that will become your map, then your map would have a SCALE of 1cm = 1m, wouldn't it?
We're not going to spend much time on it here, but, in passing... if you want "North"... magnetic, or "true", you choose... to be at the "top" of your page, you can still put "A" "anywhere". But where "B" is, relative to "A", determines the direction of both "Norths" for your map. (In my exercise, I measured and found that my baseline ran pretty nearly N/S. The north end pointed 14 degrees east of magnetic north. (That datum is not on the "fieldwork" as presented above.)
So! We have the start of our map! We have a piece of paper with "A" and "B" shown on it.
"All" we need to do is to copy the angles from the fieldwork to the map, and extend the lines from "A" and from "B" towards "C", until those lines cross. Where they cross is "C"'s place on our map!
If you work very carefully, it is easy enough to transfer the pinholes across to the map. Depending on the sizes of things, you may need to add extra paper to the map, but that's not difficult.
Alternatively, you can use a protractor to "copy" the two angles from fieldwork to map.
When the distance from A and B to C is much bigger than the length of the baseline, if either of your lines... the ones from the angles out to "C"... is even a TINY bit "off", it changes the position of "C" radically. (Think about it. You should see what I mean, why what I say is true.)
If the distance between A and B is not much smaller than the distance from them to C, you can get pretty good results this way. Especially if you have a lot of craftsmanship, and do the drawing parts very well.
Perversely, it is precisely when the distance to C is much bigger than the length of the baseline that the whole exercise is the most fun!
However, in those circumstances,
By the simple techniques given above, I got a distance to C (from A) of 1104m on 9 June 2022... for something that maps.google.com suggested should be 1950m. Yes, I was disappointed. But not down-hearted. It could have been worse. At least my angles dictated lines which converged. If they'd been even a bit "off" in the other direction, I wouldn't have had a triangle, "C" would have "been" infinitely distant from my baseline.
I offer a simple page with images relating to simple drawing the map from the data.
Other approaches, though not so easy to "follow" exist, to get you around this difficulty!
I said "never fear". Don't fear that there is no answer to the problem. (You may allow a little fear of the mathematics involved, but I am going to take you gently by the hand, lead you through them.)
For the next few sections, I am going to talk repeatedly about "the angles". I will be talking about the angles shown above as angle BAC and angle ABC... The angles at the ends of the baseline, the angles between baseline and the distant "thing" at "C" that you can add to your map after you have decided where "A" and "B" are on your map.
First... copying angles...
There are various ways to directly copy the angles from the fieldwork to the map. You should be thinking all the time, while reading this. If you are thinking, I suspect I need say little more here, as far as the direct copying approach is concerned. I've discussed it a lot in other pages, anyway.
I haven't mentioned an easy low tech answer: Use a protractor. Two problems: It is hard to measure very precisely with a small protractor. It is hard to get a good big protractor. And for each angle, you have to "read" it from the fieldwork, and then "write" it onto the map... TWO chances... for each angle... for errors to creep in. But "by protractor" WILL WORK. Work quite well, to "map" things in a field.
And then there are the "no angles" ways.
Well... it all still hinges on the angles. But you don't "draw" them on the map quite as you would if using the more obvious approach. In fact, in the first "no angles" method, you don't draw a map at all, of all you want to know is how far it is to C.
There's something called the law of sines that will be helpful. (We'll also use the law of cosines.)
The following is a general introduction. Study it, and then we'll return to our specific case...
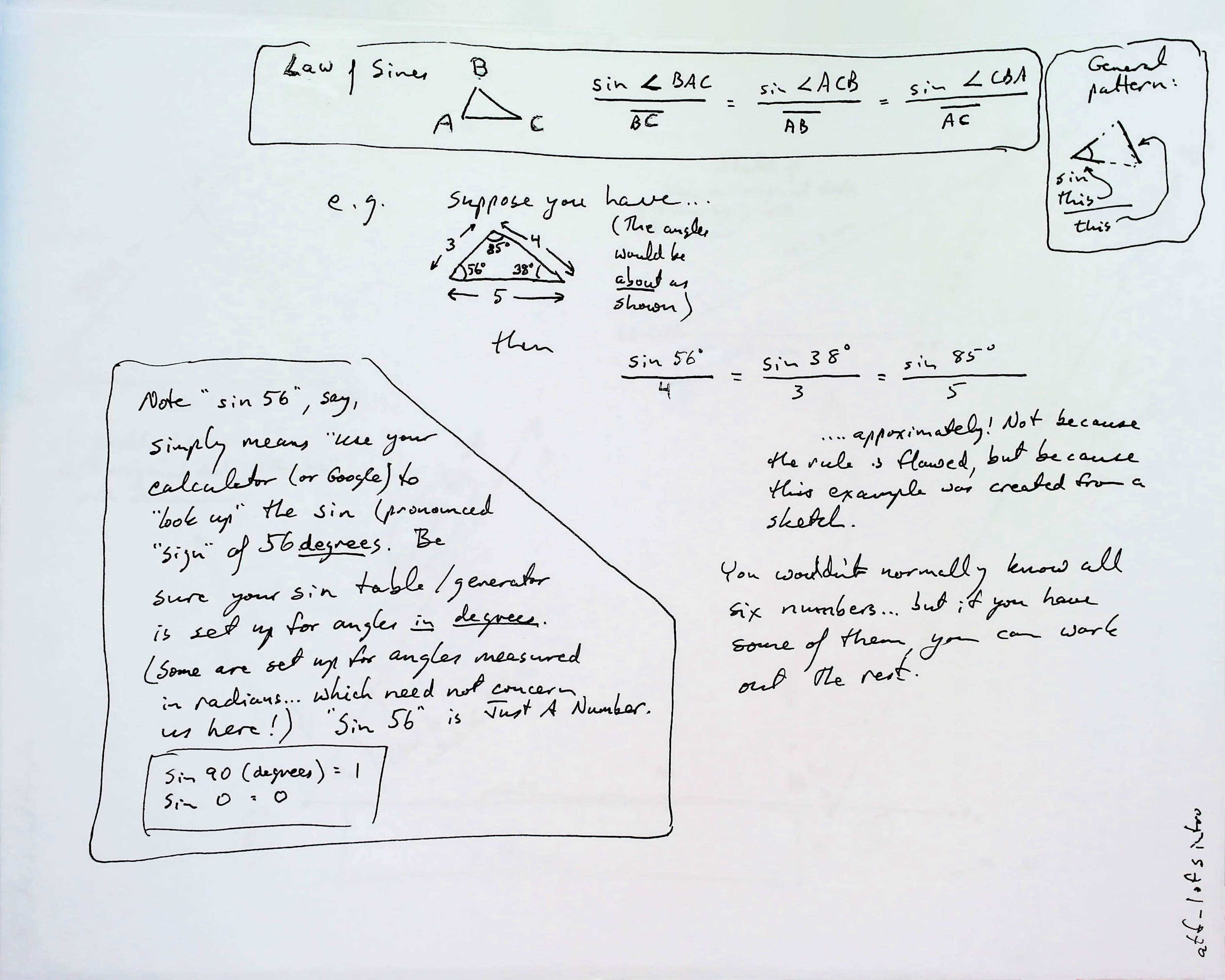
And now, for how we can use that for our purposes...
Both are started by drawing a line across the arms of each of "the angles". ("The angles" as defined above.) You convert two open "V"s to triangles, by adding a side opposite the corner the angle is in. You put it as far "out" as you can.
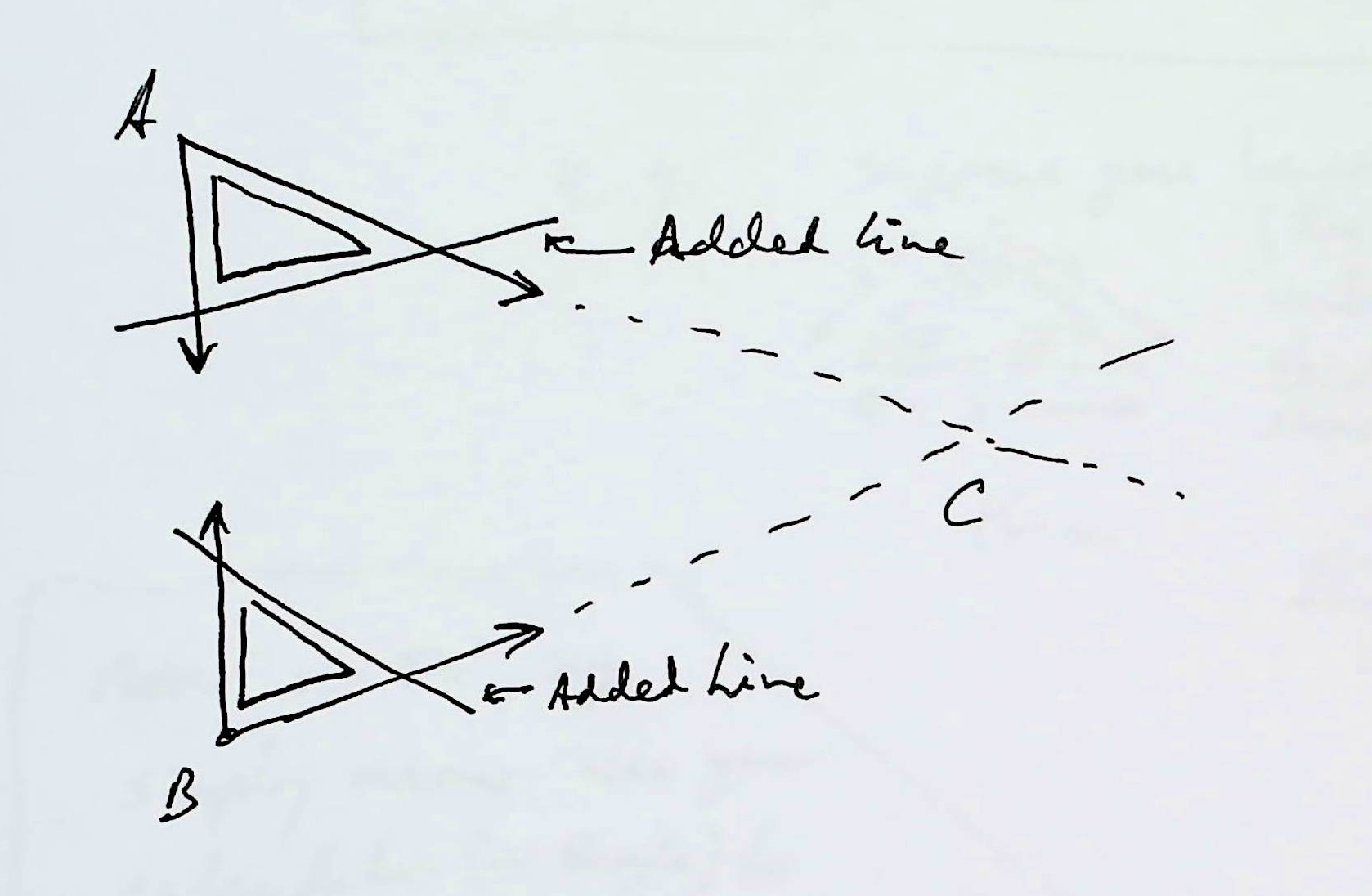
You're going to go through all the long calculation twice... once for the angle CAB, once for the angle ABC. I'll talk you through one of them.
Now measure the length of each side.
(My thanks to Wikipedia for the diagram above.)
From those numbers, you can... with "law of cosines"... calculate the size of all of the angles in the two triangles you have created. But happily, you only need one from each... The CAB and ABC angles. (The law of cosines can be used in other ways, too, but that's the trick useful to us here.)
The previous diagram was a very simplified indication of how the two corner angles might "give birth" to two triangles, upon which we could apply the rule of cosines.
The next diagram shows the actual angles I was dealing with... note that angle ABC is obtuse (greater than 90 degrees), not the "nice tidy" acute angle it has been shown as elsewhere. The real world can be so messy!. ("Monell"... it should be "Monel" is just a building)
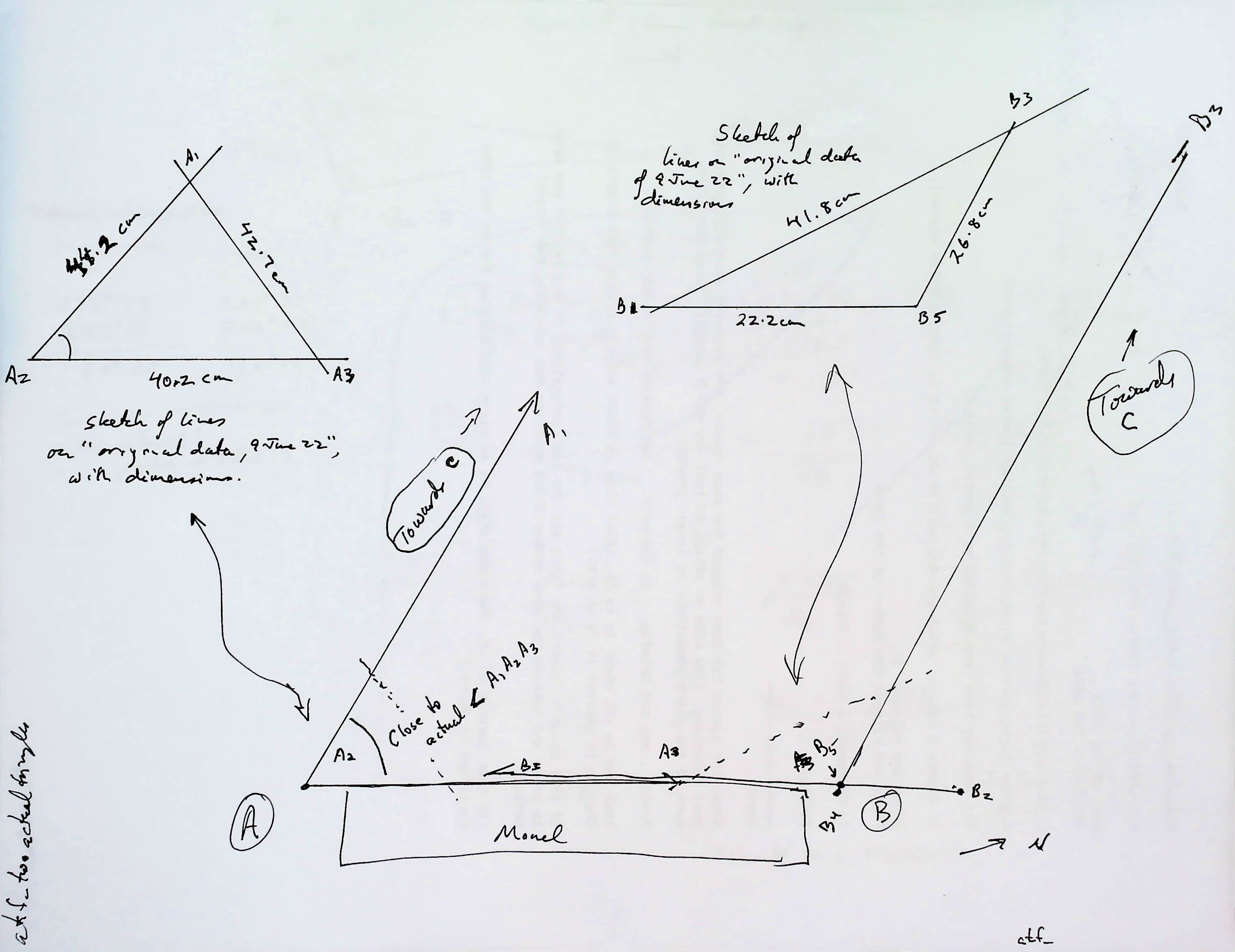
And below here we have something that needs many labels changed, but is meant to help you see how the law or sines lets us work out the side we usually call "BC" is, from our figures, 50,489cm (504.8m) long. (It is "YZ" in the diagram below.)
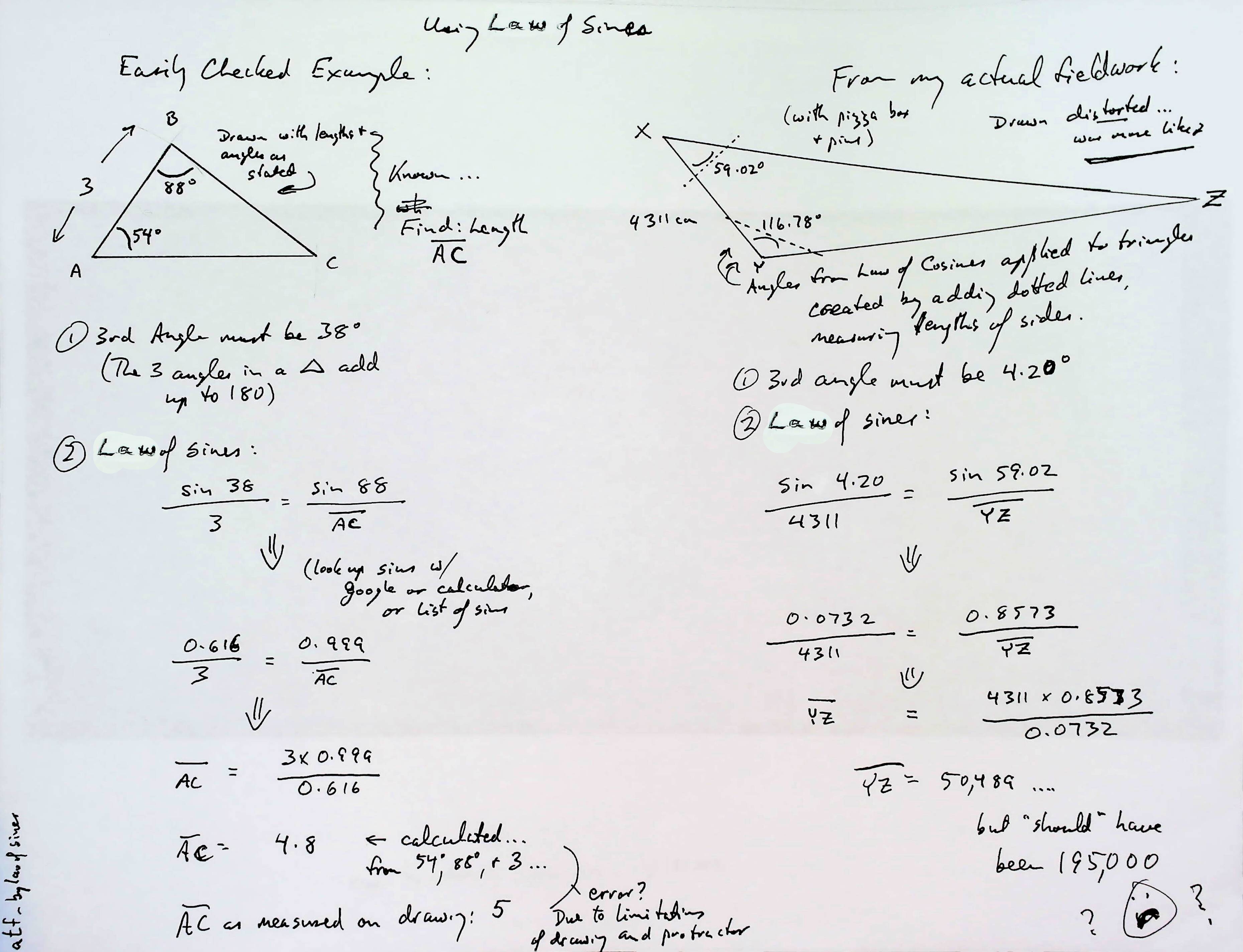
With those angles...
With angle BAC and angle ABC, and the length of the base you can, using the law of sines, calculate either AC or BC (or both)... No drafting skills required! Her are the details.
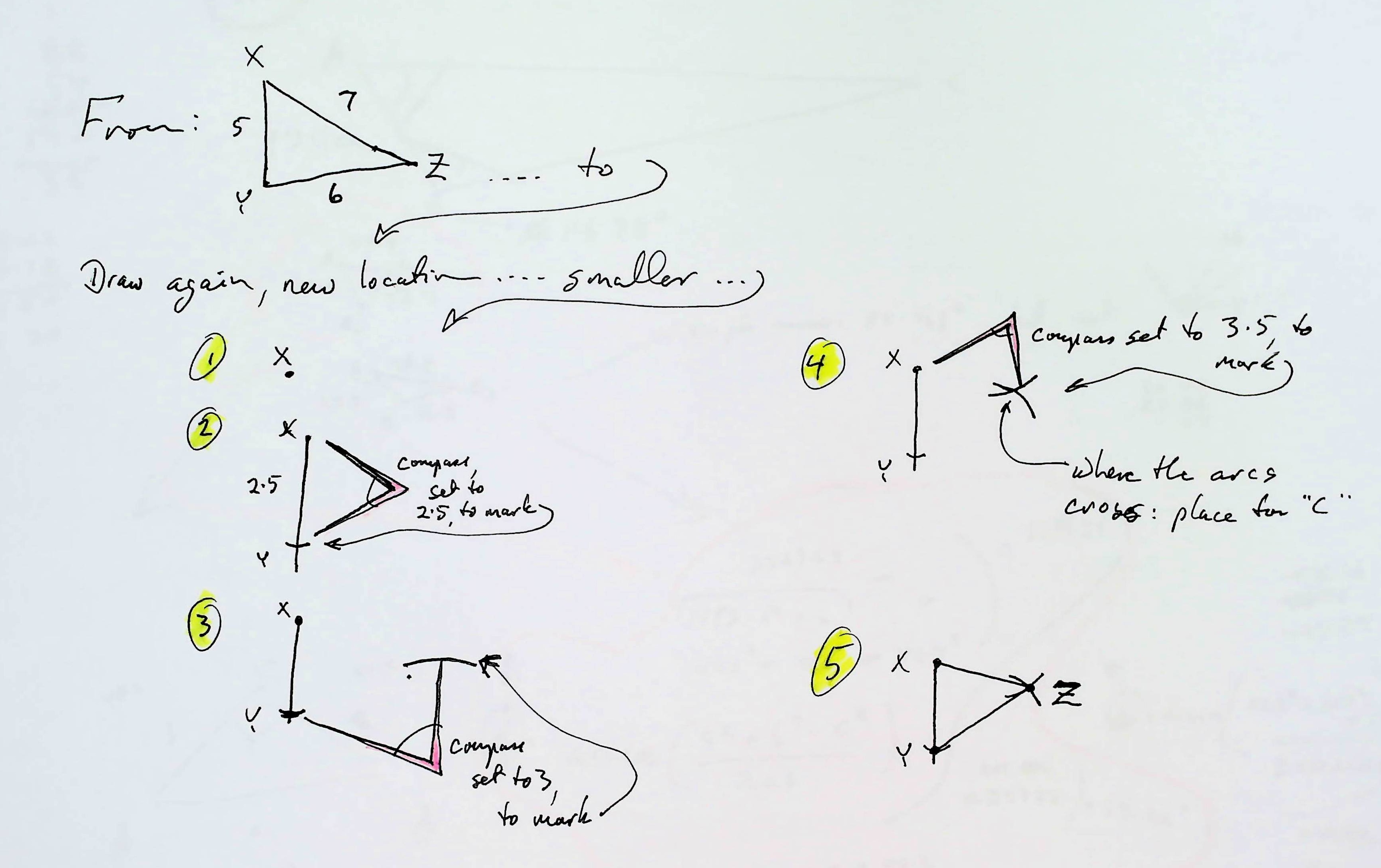
Alternatively, you can use the lengths of the sides of the triangles to "construct" the same triangles on your map. Lay them down right, and you will have angle BAC and angle ABC where you need them to define the lines which eventually cross, and determine the right place on your map for "C". (this is another "to be expanded later" thing! WHAT BIT do YOU "need" most, soonest? Contact details at bottom, and please cite "" if you write.)
**MORE TEXT**
Or use a theodolite!...
No pizza box required! But, of course, this approach starts with "catch your theodolite". (I'll address that in a moment.)
(A theodolite is the instrument that is usually mounted on a tripod, and is used to measure the angular "distance" between two bearings.)
You set the theodolite up at "A", measure angle BAC.
Then you set it up at "B", measure angle ABC.
And measure the length of the baseline as before. Here are the details, using the theolodite readings of the two angles at the baseline...
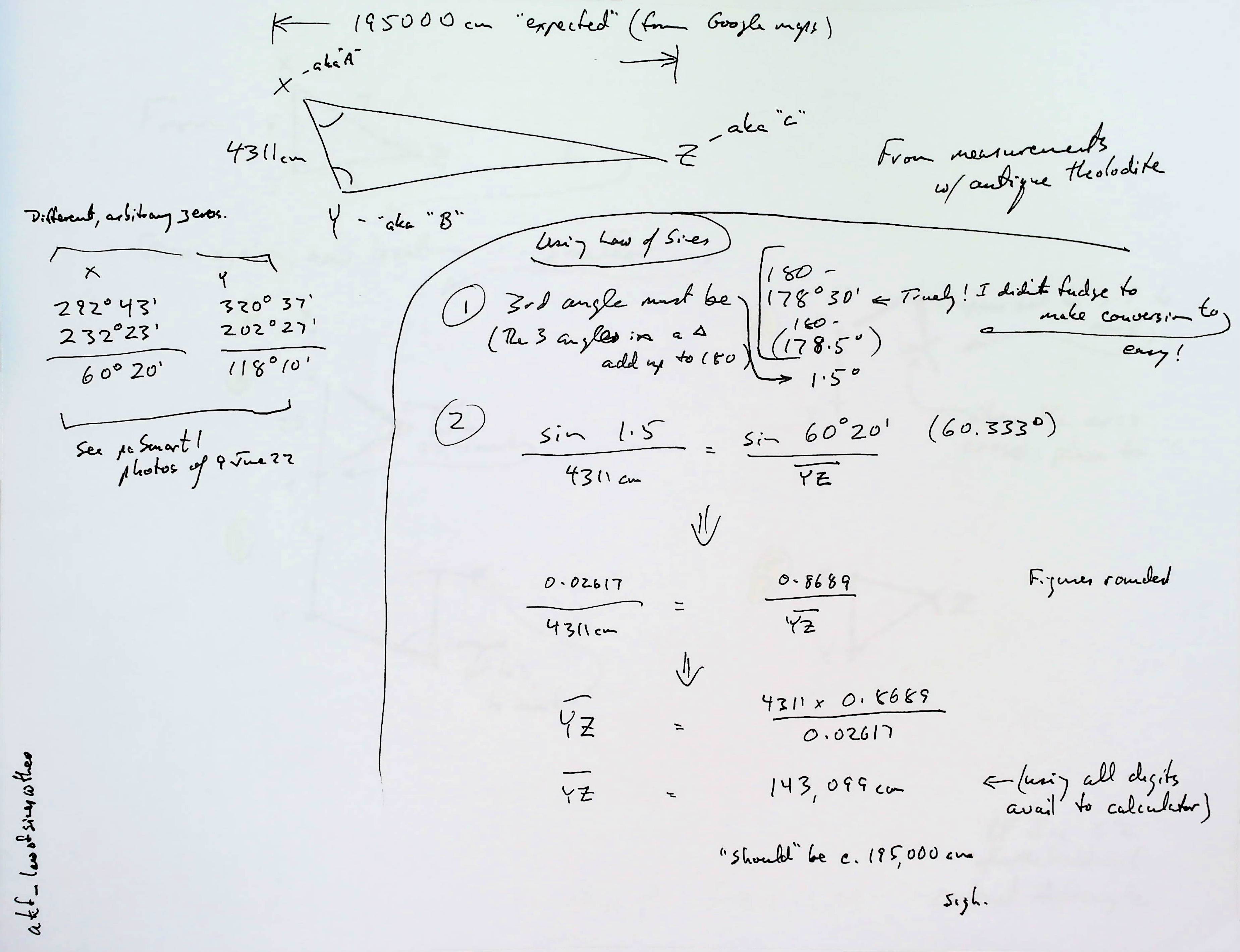
Fieldwork done! If you have a theodolite.
I've been interested in all this for many years. At an auction along the way, I was lucky to pick up a gorgeous old theodolite in perfect working order, for a fraction of what it would have cost "back in the day". It took a bit of head scratching to figure everything out, but I think I now understand the essentials.
Using my antique, I measured the same angles as I captured with my pizza box.
The following image has "the wrong names" on the points of our big triangle. I hope you can see that X stands for what has been called "A" elsewhere, Y is B, and Z is C. (XY is the baseline.)
IMAGE TO COME
The diagram shows (left side) the bearings I took with the theodolite from A and from B. (Two bearings from each... one to "C" and the other to the other end of the baseline. Subtract bearing to C from bearing to other end of the baseline, and you get the angle... In this case 60 degrees, 20 minutes for angle CAB and 118 degrees, 10 minutes for ABC).
From the two angles, and the length of the baseline, again using the law of sines, we can calculate the length of either AC or BC. I did the maths for AC.
It came out at 1431m.
When I did it by "drawing alone", not explained in detail here, I got 1084m for AC
So... by the three methods presented here, I got 1431m, 504m and 1084m for AC... a distance which, from maps.google.com, seems to be about 1950.
Was I disappointed? Of course! But not downhearted. I'll go back again one day, do the fieldwork again... more carefully! I'll double check my arithmetic. (This page has been pushed out when I SHOULD have been doing other things.
I've done mapping by the "draw it" method for years... with some very good results. (Using my home-made ($25) theodolite.)
This is the first time I've used my antique. It is the first time I've used all the fancy arithmetic... for which thanks are due to a very good, very old friend. When I knew what I wanted, he supplied answers ("The law of sines, the law of cosines" instantly!) We shared a room at boarding school. He subsequently taught mathematics there for 38 years. My whole... interest? (some use an less kind word!) with mapping started there, from an offhand comment by a wonderful teacher... in 1968.
I strongly suspect that some of the variation is due to errors in my arithmetic. But it is interesting that two answers are wrong by about the same amount. Where do you think I made the mistake that explains that?..
v
... answer in a moment... don't scroll 'til you finish trying to figure out for yourself where I might have gone wrong, causing those results....
v
v
v
v
v
v
v
Did you "get it"? One possible thing that would give those results would be a mistake over the length of the baseline. Alas, Google gave me the same figures for the baseline, within the limitations of that source, as I had recorded when I was doing my fieldwork. Just one of life's little mysteries, I guess. (I haven't redone all the sums... yet. I may have a happy surprise in due course, I suppose.)
Another possibility...
I started my fieldwork by driving two stakes into the ground. They marked my real world "A" and "B". I suspect that I wasn't sufficiently careful to have the "A" on my pizza box precisely over the stake while I was capturing angle CAB. I may also have failed to do a good job of placing the pin that was SUPPOSED to indicate the direction line AB went from A to B. (And that I made the same sorts of mistakes at the other end of the baseline: pizza box "B" not directly over real world B, line towards A not lined up sufficiently carefully.)
And then, when I measured the angles with the theodolite, similar errors could have been made... though one of the joys of using the theodolite is that such errors would be harder to make.
Tiny errors in any of these would affect my results.
And of course, I may have made some errors along the way when doing calculations!!!
Going back to "catch your theodolite": You could, of course, make your own! I've done a guide to this. Try to enter into the spirit of how the guide was written. What's the fun of just being told? The guide invites you to figure the problems out for yourself... but gives you hints, and eventually gets you all the way from concept to design.
As I said... I've been having fun with all of this for a Very Long Time. Perhaps the best "index" to my stuff, at the moment, is...Flat Earth Academy- Geography Topics.
If you found this of interest, please mention in forums, give it a Facebook "like", or whatever. If you want more of this stuff: help!? There's not much point in me writing these things, if no one hears about them. Does anyone feel they are of any use? If YOU do- please spread the word!
Search across several of my sites at once with a Google search button.
Or...
Or...
What's New at the Site Advanced searchUnlike the clever Google search engine, this one merely looks for the words you type, so....
* Spell them properly.
* Don't bother with "How do I get rich?" That will merely return pages with "how", "do", "I"....
Please also note that I have three other sites, and that this search will not include them. They have their own search buttons.
It's both! Flat-Earth-Academy.com is something I started years ago. For a variety of reasons, I can't offer you httpS:// access there. (As you are not asked to input any information, that's moot, but it "worries" search engines.) So I'm moving to my new, all singing, and will do the httpS:// dance site, "WYWTK.com", and Flat-Earth-Academy is gradually acquiring pages there. (Well, HERE, as what you are reading is one of my "wywtk/fea" pages.)
Why "WYWTK"? It comes from "What You Want To Know".
Page has been tested for compliance with INDUSTRY (not MS-only) standards, using the free, publicly accessible validator at validator.w3.org. It passes in some important ways, but still needs work to fully meet HTML 5 expectations. (If your browser hides your history, you may have to put the page's URL into the validator by hand. Check what page the validator looked at before becoming alarmed by a "not found" or "wrong doctype".)
AND tested for
. . . . . P a g e . . . E n d s . . . . .