Before I explain the challenge, a word about the inspiration for it.
But for the code-breaking work at Bletchley Park in the 1930's and 40's, it is likely that the Nazis would have over-run Britain. Of course other efforts contributed, indeed were equally critical.
This challenge touches on a TINY part of what was being done at Bletchley. I hope attempting it will give you food for thought. (By all means read this with a view to becoming inspired! Do your own thing, if a think occurs to you. I don't mean to say "you must do this, this way"!)
Reflecting on what was accomplished at Bletchley may raise the hairs on the back of your neck. Especially if you recall that they didn't have modern electronics. Not even a transistor. or even some of the ideas used below.
The work might also be useful to you in other ways, although there are more direct routes to things you will learn along the way here.
I hope you attempt this using an Arduino or similar. Where I say "Arduino" in what follows, take it that I want you to infer "...or similar" every time.
Alternatively, elements of the challenge can perfectly well be done in a big computer with just a keyboard and a monitor. But it won't be as much fun like that!
This page turned into too many words. Here's a sketch of what follows...
The page says, with a little help with how to do it...
Here's a challenge:
Take some simple text. Substitute numbers for the letters.
Express them as binary numbers.
Add a start bit, a stop bit.
Build...
a) a program for keyboard and monitor to accept text and deliver 1's and 0's, and/or an asymmetric square wave.
and/or
b) set up an Arduino to "wink" an LED with some text as a stream of bits.
and/or
c) (having done "b") set up another Arduino to turn the 1's and 0's "b" is making back into text.
No encryption going on at all... yet. This is "phase 1" of a bigger challenge project.
For large parts of this the connection to secret codes will not be clear. In parts I will greatly simplify things.
Bear with me? There IS a point to what you are invited to attempt. And it IS related to the Lorenz code, which the Colossus machine helped to break. It also has application in many things you may one day want to do with a computer.
I'm not going to tell you EVERYTHING you need to consider. Where would the fun be in that? (I often do write tutorials about making Arduinos do things and programming in general. They do try to tell you everything.
Here I'm offering a challenge, which I hope you will find fun. I've told you enough to create a valid entry in the competition.
Prizes: First prize will be half of what I've been paid in the last six months for this essay. 2nd prize: half of what I've been paid in the past 4 months. 3rd prize: half of what I was paid for this essay in the two months before that.
Don't spend your prize money yet. It won't be very much. Possible the number you get if you take 2 squared + the square root of 25 away from 9.
Consider the phrase...
THE CAT SAT ON THE MAT.
Pretend you want to send that as a radio signal... but by some system other than Morse code, or speech.
First we turn each letter and punctuation mark into a decimal (everyday) number. The following aren't the actual numbers used in the Lorenz system, but they'll do for our purposes. Write you program so that it is easy to switch to a different table for assigning the characters to numbers.
We'll use...
(space) A B C... Z (period) 0 1 2 3... 26 27 (Full table at bottom)
For reasons you may grasp in a moment... and if you don't, don't worry, we can only use 0-31. I've allocated 0-27 in the table above. 28-31 could be used for other punctuation marks.
Note that we have not provided a way to show digits. I.e. 0, 1, 2.
There is a way, but it doesn't need to concern us here. ("The way" does NOT entail using numbers bigger than 31.)
(All of what we are doing CAN be modified to allow numbers bigger than 31. The usual "next level" allows numbers up to 127, and often a designer will choose to go to 255 if he/she considered going to 127. Forgive me not going into the reasons? But these are not numbers drawn from a hat!)
For our purposes, we would use ZERO, ONE, TWO... to send digits... as in...
ONE CAT SAT ON THE MAT
--- So far so good? By the system given...
THE CAT SAT... ...becomes...
20 8 5 0 3 1 20 0 19 1 20
(The space between the words is just another character, as far as all of this is concerned. And 20 is the number for a space.)
Here in principal, though with a different mapping of letters to numbers, and simplified for the moment, is what Lorenz did with those numbers...
Each number was turned into an equivalent number consisting of five 1's or 0's. The usual (to mathematicians!) way of saying that is that they turned each into an equivalent 5 bit binary number.
If "binary" is a mystery to you, don't worry... there are tables you can use. There's one at the bottom of this page. Here's a part of it...
(In this part of the table, we have the "ordinary" number before the colon, and the equivalent 5 bit binary number after it.)
0: 00000 1: 00001 2: 00010 3: 00011 4: 00100 ... etc, etc. (Full table at bottom)
Using that, THE CAT...
20 8 5 0 3 1 20
... comes to...
10100001000010100000000110000110100
Don't worry about why some of the bits are red... I've done that to help you see the groups of five. I've used the colors simply to make it easier for you to see where each character's binary representation begins. In practice, a red 1 and black 1 are "just" a 1, no different from one another.
Notice that nothing goes between the end of the 1's and zeros for one character's representation and the start of the same for the next character's. ("Bit" at the start of this paragraph used in the narrow sense: Bit= a one of a zero. I've tried NOT to use it in the general way anywhere in this essay apologies for any lapses.)
And yes, if you wanted to send THE CAT SAT ON THE MAT in a form that wouldn't be readable to an eavesdropper, you'd have to add more steps.
All we're trying to do for the moment is see how letters might be sent by over wires or a radio link.
To send that, what they did, almost, was to work from left to right, sending a short burst of a high pitched noise for each "one" and a short burst of a low pitched noise for each "zero". (The length of the bursts had to be quite precisely controlled, so they were all of the same duration.)
For our discussions, we'll pretend that each 1 or 0's note lasted for 1 second. (Of course, in any real system, you wouldn't stretch each one out so far.)
If you are attempting the challenge as text on a big computer, the time/bit isn't relevant. But your simulation is a little further from the Lorenz encrypting.
If you are working with an Arduino, add a switch that can tie an input high or low. Program the Arduino so that...
If the input is high, make each bit last a second for demonstrating it working at a speed a human can read.
If the input is low, make each bit last 80ms, for Arduino sender to Arduino receiver demonstrations.
---
We've made a lot of progress!
If you are doing this with a program on a big computer, if you can turn a bunch of characters into a string of 1's and 0's, you've accomplished a lot.
If you are doing this on an Arduino, I'm going to challenge you to set one up with two momentary switches and 1 LED.
Press the first button, and the LED should wink the 1's and 0's which stand for "THE CAT SAT ON THE MAT". Press the other button and the LED should flash the 1's and 0's that stand for "PPPPPWWWPPPPPWWW", repeated three times... which is gibberish, but it gives a pretty distinctive pattern of LED winks... if your system is doing what it should! (^_^)
For reasons you may be able to figure out, which I hope someday to spell out for you (but it won't be today)...
With a system like this, it wasn't five 1's and 0's for each character, but seven.
BEFORE the 5 bits (1's or 0's) we've already talked about, there was always an extra 1. This was called a "start bit".
And AFTER the 5 we talked about above, there was always an extra 0, called a "stop bit".
So now, THE CAT looks like...
1101000100100010010101000000100011010000101101000.
The underlined 1's are the start bits in the data stream. You can see that as you should be expecting, (apart from the start bit at the start of the text,) each start bit (always a 1) is preceded by the stop bit (always a 0) at the end of the 1's and 0's of the previous character in the string.
In the Arduino version of this, make it turn the LED off whenever it is not sending characters.
If you think about it, it means that there will always be a change from a 0 to a 1 between any two characters. This is A Good Thing.
--- We've made a crude sender! Even if it doesn't yet change our message into a scrambled version which would mean nothing to an eavesdropper.
Imagine trying to make such a thing in 1935!
--- Can you make a receiver? For the big computer version, you need to type the 0's and 1's from the sender program into the receiver program, and it needs to give you back whatever was sent. (Or you can have the sender write the 0's and 1's to a file, have the receiver read the file. Or the sender can send them to a memo box on the screen, from which a "receiver" module in your challenge submission can fetch them.
For the Arduino, ideally you will set up a second Arduino, feed the LED driving output of the first to the second, and have the second send the received characters to the serial terminal.
--- All of this was truly one essential ingredient of the Lorenz system.
--- I wish you well with the challenges. I hope you will send reports of your success by whatever means you like. The easier you make it for me to showcase your submissions, the better your chance of fame. I can't promise much fortune. YouTube videos would be great. Source code for others to admire would be great. Etc.
--- Remember I said that the Lorenz system used high and low tones? You also need to know that a bit was only transmitted for a very short time. No human could record what was arriving so quickly. Nor, then, could anyone build a machine to write, say, "THE CAT SAT..." as it arrived.
So the clever boffins created a machine to "draw a picture" of the highs and lows which were coming in.
Lets say you wanted to send the following...
110110-1001010-1011000- 1011000-1000000-1100110- 1100000-1011110-1101000- 1101000-1001010-1001000- 1110110
I've written out the sequence of 1's and 0's a message might consist of. The hyphens wouldn't be in what the receiver heard. They are there to help you distinquish the characters. (Can you figure out what they stand for?!)
I've included the start and stop bits. The first group (6 1's and 0's) has one less than others because they include stop bits from previous characters.
... the "picture" the machine would draw from the corresponding stream of squeaks would look like...
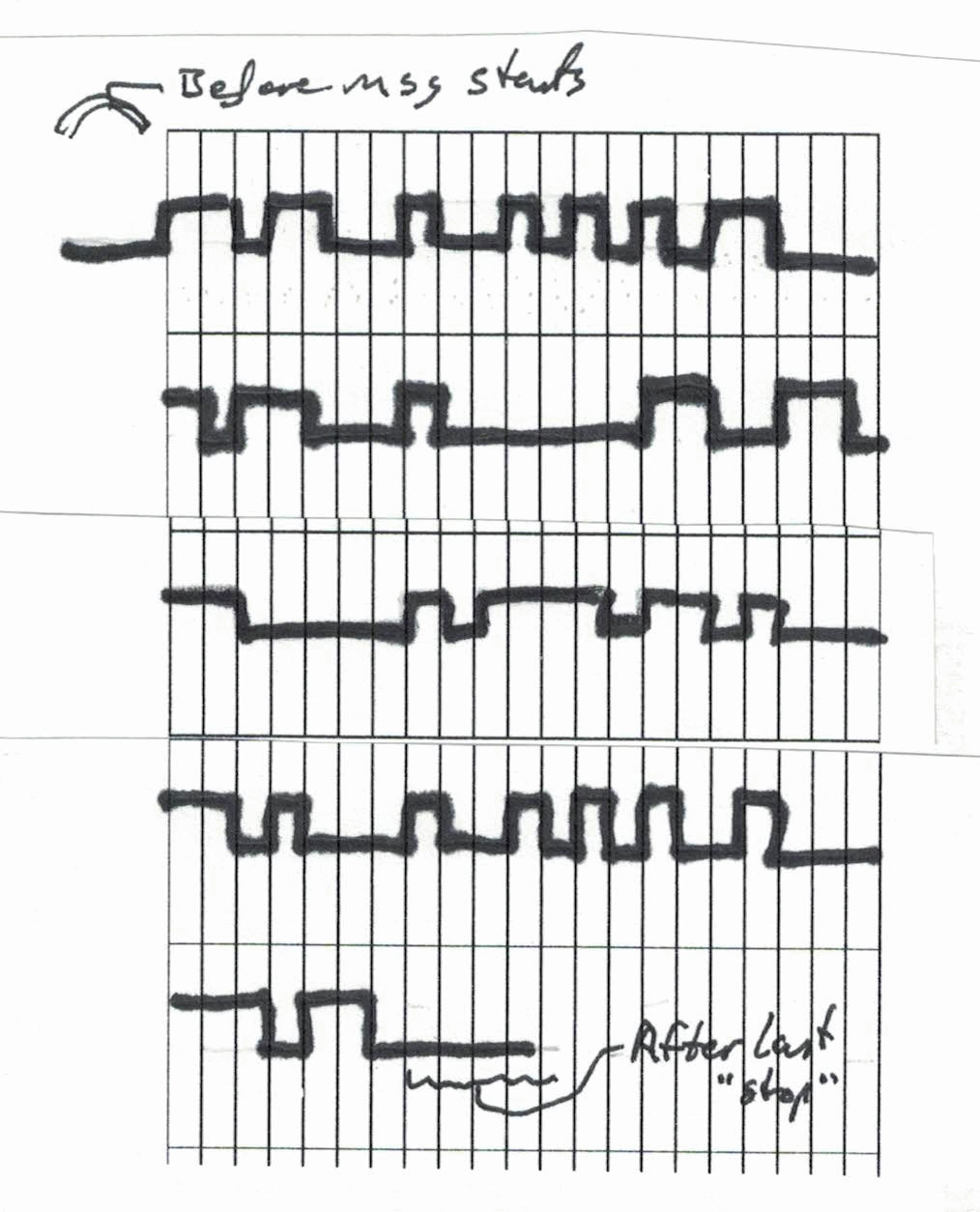
Scores of typists spent thousands of hours looking at such "pictures" and, by eye, picking out the groups of seven bits (start+data+stop), and from memorized tables of all the 32 possibilities, typing the characters represented by the groups of seven bits.
Amazing but true.
And today, you can make a simple, inexpensive computer (Arduino, Pi, etc.) do these jobs...
1) Turn messages ("THE CAT SAT...") into squeaks, or an LED winking.
2) Turn a digital input... from the winking LED, say... back into "THE CAT..."
N.B.: In much of this, I am not including any encryption! During WW II, of course they didn't go to all this trouble to send "THE CAT SAT...". They just used Morse Code.
For sensitive messages, they turned "THE CAT SAT..." into a string of other characters, gibberish, and sent THOSE to the other end. Where they were turned back into the string of gibberish, and then reversed the encryption step. How the Lorenz encryption worked is a different story. In this essay, we're just working on how letters... any letters... were sent and received.
Or you could at least imitate the first process on a complex, expensive computer! Get it to turn text into strings of 1's and 0's. If you manage that, have it save them to a data file, and then write the program to reverse the process.
If you are attempting the challenge on a big computer, you can have extra credit if you make your program draw the "picture" (as above) for whatever you type in.
What we've done before does not send something that an eavesdropper would have trouble turning into characters.
What I am going to sketch here wouldn't but a very big stumbling block in the path of an eavesdropper, but it indicates how encryption might be done, and another time I'll write about something which would be harder to decrypt.
So far we have...
Before I go further: If I say "complement the bit" (not compliment!), I mean: If it is a 1, make it a 0.
To make that opaque to an eavesdropper, between 2 and 3, add a new step...
Without touching the start and stop bits, go through the message.
In the first character, complement the first bit
In the 2nd character, complement the 2nd bit
In the 3rd character, complement the 3rd bit
In the 4th character, complement the 4th bit
In the 5th character, complement the 5th bit
When you get to the 6th character, you go back to complementing the 1st character.
Not hard. You're still left with just 1's and 0's, which you send to the recipient however you sent them before.
But! Now what you are sending isn't easily changed into the message you don't want the eavesdropper reading.
Image you wanted to send "AAAAAAAA...". (I don't know why you would, but imagine it.)
If we used the extra steps just explained, an eavesdropper would NOT see one letter over and over. He/ she would see a jumble of letters. Clever, eh? This simple ruse would encode sensible messages too. (We will look at more sophisticated encryption algorithms later.)
What I've proposed adding to the sending is not hard for the recipient to reverse. This is because if you complement a one or a zero, and then complement the result, you end up back where you started! So complementing bits the encrypted text with the same rule you used to encrypt the plain text takes you back to the plain text.
What encryption rule would be better?
I've written second page discussing a more secure encryption rule. It can only be applied to a string of 1's and 0's. I hope the page you are reading has made you comfortable with the details of turning text into and out of strings of 1's and 0's?
This challenge arose out of the wonder evoked in me by seeing the machine that helped decrypt Lorenz encoded messages. They were traveling via radio signals, and this has led to a bias in this challenge.
Taking a message, turning it into a lot of 1's and 0's, and then doing things with them is generally useful. However, the 1's and 0's could be turned BACK into characters at this stage, typed onto a piece of paper... the characters would look like gibberish... that piece of paper could be sent through the mail to a recipient, who would then recover the original message. There's nothing magical or necessary about using radio waves, or 1's and 0's for the sending.
If, however, you want to send the message through wires from one machine to another, then the 1's and 0's are ideal, of course.
We've looked in detail about how characters can be turned in to groups of 1's and 0's.
In the above, we contented ourselves with just 32 possible characters. There's no need to be so parsimonious. A bigger set of characters can be used if you decide to have more than 5 bits carrying data. Having just 5 restricted the range of characters we could use... and indeed the Lorenz used only 5. Using more would not have introduced new ideas, it would simply have made the strings of 1's and 0's in the examples longer.
We've seen what we need to do with individual characters.
Now let's think about the sending of phrases.
If we don't require that the sending machine and the receiving machines be always "in step", life become easier in some respects. On the other hand, if we want the simplicity of using just one wire between them, a bit of cleverness must be introduced.
I'm going to use the work "message" for a group of characters. For our simple purposes here, we will agree that the characters are encoded as they were before... a start bit, 5 data bits, and a stop bit.
Remember that the start bit is always a 1, the stop bit is always a 0.
When the sending machine is not sending, it should make the state of the wires between the machines 0.
So... if the receiving machine has been off doing other things, and has just now returned to the wire signals come in on, it's DataInput line, and it finds it is showing 0 at the moment, does that mean that the sender isn't sending? What if the sender IS sending, but the bit it is sending just now is a zero?
Here's the bigger story...
When the receiver starts watching DataInput, it, for the moment, assumes that the sender is in the middle of a message. There is no simple way for the receiver to read the rest of that message.
It starts a timer. And it restarts it every time DataInput changes from a 0 to a 1. We call thus "going high".
If the receiver doesn't see DataInput high for a bit more than the time it would take 7 (in this scenario) data bits to pass along the wire, then it "says", "Ah! The sender isn't sending at the moment."
The receiver continues to check DataInput. If, as proposed above, each bit is "put" on DataInput by he sender for one second, as long as the receiver checks DataInput several times per second, that will be enough.
Once it has established that the sender was not already sending a message the last time it started its timer, then the receiver watches for a start bit... a 1. It then lets 1/2 a second pass, and then one second pass. It will now be somewhere in the first data bit. It reads DataInput. It waits a second. It will now be somewhere in the second data bit. And so on. When it gets to what should be the stop bit, it goes back to looking for a "1". At that point it again does the "throw away a half second, wait one second" to get itself back to adequately in step with the signal as sent by the sender.
You'll never (by simple means) get sender and receiver extremely close to being in step. But by the grace of start and stop bits, being "close" is going to adequate for the system to work.
Never solve a problem when there is an easy way around the problem!
=========== The tables...
(space) 0 00000 A 1 00001 B 2 00010 C 3 00011 D 4 00100 E 5 00101 F 6 00110 G 7 00111 H 8 01000 I 9 01001 J 10 01010 J 11 01011 L 12 01100 M 13 01101 N 14 01110 O 15 01111 P 16 10000 Q 17 10001 R 18 10010 S 19 10011 T 20 10100 U 21 10101 V 22 10110 W 23 10111 X 24 11000 Y 25 11001 Z 26 11010 (period)27 11011 (avail) 28 11100 (avail) 29 11101 (avail) 30 11110 (avail) 31 11111
Please get in touch if you discover flaws in this page. Please mention the page's URL. (wywtk.com/ardu/lor/lorenz1a1.htm).
If you found this of interest, please mention in forums, give it a Facebook "like", Google "Plus", or whatever. If you want more of this stuff, help!? There's not much point in me writing these things, if no one feels they are of any use.
|
Unlike the clever Google search engine, this one merely looks for the words you type, so....
* Spell them properly.
* Don't bother with "How do I get rich?" That will merely return pages with "how", "do", "I"....
Please also note that I have three other sites, and that this search will not include them. They have their own search buttons.
http://www.arunet.co.uk/tkboyd/index2.htm My site at Arunet. (Not httpS- sorry!)
![]() Page has been tested for compliance with INDUSTRY (not MS-only) standards, using the free, publicly accessible validator at validator.w3.org. It passes in some important ways, but may still need work to fully meet HTML 5 expectations.
Page has been tested for compliance with INDUSTRY (not MS-only) standards, using the free, publicly accessible validator at validator.w3.org. It passes in some important ways, but may still need work to fully meet HTML 5 expectations.
....... P a g e . . . E n d s .....